프로그래머스의 파괴되지 않은 건물(Lv3) 문제이다.
[ 문제풀이 ]
정확성과 효율성이 있는 문제이다. 문제가 되게 간단해 보이고 간단해 보이는 만큼 간단하게 접근해서 풀게되면 정확성 면에서는 통과를 할 수 있지만, 효율성에서는 통과를 하지 못하게 될 것이다.
정확성만 통과할 수 있는 간단하게 접근하는 방법부터 효율성까지 모두 통과할 수 있는 방법까지 순차적으로 이야기해보자.
#1. 간단한 접근
그럼 가장 먼저 간단한 접근부터 생각을 해보자.
적의 공격을 받아서 내구도가 낮아지게 되면 낮아질 때 마다 단순 반복문을 통해서 해당 좌표 사이에 있는 모든 좌표들의 내구도를 낮춰버리고, 회복 스킬을 받아서 내구도가 높아지게 되면 높아질 때 마다 단순 반복문을 통해서 해당 좌표 사이에 있는 모든 좌표들의 내구도를 높여주는 것이다. 너무나도 간단하게 단순 2중 for문을 통해서 다음과 같이 구현할 수 있을 것이다,.
vector<vector<int>> MAP;
void Process_Command(vector<vector<int>> Skill) {
for (int i = 0; i < Skill.size(); i++) {
int S = Skill[i][0];
int x = Skill[i][1];
int y = Skill[i][2];
int xx = Skill[i][3];
int yy = Skill[i][4];
int Value = Skill[i][5];
for (int a = x; a <= xx; a++) {
for (int b = y; b <= yy; b++) {
if (S == 1) MAP[a][b] -= Value;
else MAP[a][b] += Value;
}
}
}
}위와 같은 형식으로 2중 for문을 통해서 구현을 할 수 있을 것이다. 실제로 이렇게 구현을 하더라도 정확성 부분에서는 pass를 받을 수 있다. 하지만, 이렇게 구현하게되면 효율성 부분에서는 시간초과가 발생하게 된다.
지금부터는 시간초과가 왜 발생하게 되는지부터 알아보고 이를 어떻게 해결할 수 있는지에 대해서 이야기해보자.
#2. 정확성과 효율성
먼저, 이 문제에서 최악의 상태로 입력이 주어지는 경우를 생각해보자.
여기서 최악의 상태라는 것은 "최대범위에서 가장 많은 데이터를 이용해서 실행했을 때"를 의미한다.
정확성 테스트 케이스에서 최악의 상태는 어떻게 될까 ??
"맵의 크기가 100 x 100 의 형태일 것이고, skill의 행의 길이가 100인 경우" 일 것이다.
왜냐하면, 정확성 테스트케이스에서 맵의 행의 길이와 열의 길이의 최댓값은 100이고, skill의 행의 길이가 100인 경우가 최대라고 제한되어 있기 때문이다. 더 나아가서, skill이 [ type , r1 , c1 , r2 , c2 , degree ] 형태로 주어지는데, 이 때 100개의 Skill이 모두
(r1 , c1) = (0 , 0) , (r2 , c2) = (100 , 100) 으로 주어지는 경우일 것이다.
그렇다면 이 경우에 #1에서 이야기했던 2중 for문을 통해서 구현을 하게 되면 어떻게 될까 ??
아마도 100 x 100 크기의 맵을 100번 탐색을 해야 하는, 즉 ! 100 * 100 * 100 만큼의 연산을 진행하게 될 것이다.
결국 1,000,000만큼의 연산을 진행하게 될 것이다. 100만번의 연산은 그리 큰 숫자가 아니다.
그렇다면 효율성 테스트 케이스에서 최악의 상태는 어떻게 될까 ??
제한사항을 확인하고 위에서 이야기했던대로 똑같이 적용시키게 되면 효율성 테스트 케이스의 경우에는
1000 * 1000 * 250,000 번의 연산을 하게 된다. 즉 ! 250,000,000,000 번의 연산을 하게 된다.
숫자를 읽기도 힘들다. 저정도의 연산을 하게되니 #1에서 제시했던 2중 FOR문을 사용하는 코드로 문제를 해결하게 되면 시간초과가 발생하게 되는 것이다. 그렇기 때문에 효율성 테스트 케이스를 통과하기 위해서는 조금 다른 방법이 필요하다.
#3. 새로운 방법 - 누적합
본인은 이 문제의 효율성 부분을 해결하기 위해서 누적합 방식을 이용해 주었다.
누적합 이라는 것은 현재의 값을 기존 값 까지 합친 값을 합치는 것(?)을 의미한다.
그럼 이 누적합을 어떻게 적용할지에 대해서 이야기를 해보자. 이 문제에서는 2차원 배열로 맵이 주어졌지만 먼저 간단하게 1차원 배열을 통해서 이야기를 한번 해보자.

위의 배열에서 "0번 Index부터 3번 Index까지 모든 값을 + 2 시키세요" 라는 명령이 떨어졌다고 가정해보자.
그럼 정말 간단하게 #1에서 했던 이야기처럼 0번 부터 3번 까지 반복하면서 모든 Index의 값을 + 2씩 하는 방법이 있을 것이다.
그런데 지금부터는 저런 방법으로 하지 않을 것이다. 새로운 배열을 하나 더 만들어서 저 과정을 매우 간단하게 만들어 버릴 것이다.

위와 같이 모두 0으로 초기화 되어 있는 배열을 하나 만들 것이다.
그리고 다시한번 "0번 Index부터 3번 Index까지 모든 값을 + 2 시키세요" 라는 명령이 떨어진다면 위의 0으로 초기화 되어 있는 배열을 다음과 같이 바꿀 것이다.

이게 뭐하는 것일까 ?? 왜 0번 Index만 + 2를 시켰고 갑자기 뜬금없이 왜 4번 Index는 -2를 시킨 것일까 ???
이 배열에서 누적합을 한번 계산을 해보자.
0번 Index의 경우에는 기존의 값이 없으므로 '2' 그대로 유지.
1번 Index의 경우에는 0번 Index까지의 합 + 1번 Index 가 되므로 2 + 0 = '2'
2번 Index의 경우에는 1번 Index까지의 합 + 2번 Index 가 되므로 2 + 0 = '2'
3번 Index의 경우에는 2번 Index까지의 합 + 3번 Index가 되므로 2 + 0 = '2'
4번 Index의 경우에는 3번 Index까지의 합 + 4번 Index가 되므로 2 + (-2) = '0'
5번 Index의 경우에는 4번 Index까지의 합 + 5번 Index가 되므로 0 + 0 = '0'
위와 같이 계산이 될 것이고 위의 계산 결과를 다시 깔끔하게 그림으로 나타내면 다음과 같다.

이런 배열이 만들어 지게 되었다. 그럼 "0번 Index부터 3번 Index까지 모든 값을 + 2 시키세요" 는 언제 계산할 수 있을까??
원본의 배열과 계산을 위해 새로 만든 배열 2개를 한번 더해보자.
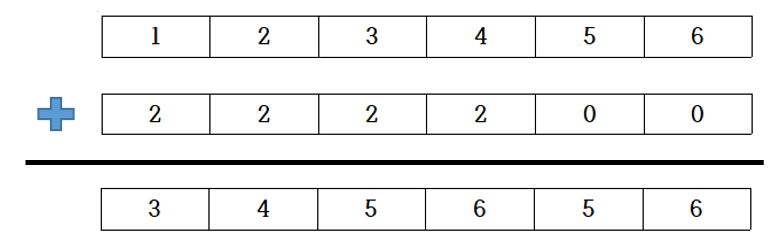
위와 같이 결과가 나오게 될 것이다. 이 때, 0번 Index부터 3번 Index에 주목해보자.
우리가 원하던 "0번 Index부터 3번 Index까지 모든 값을 + 2 시키세요" 와 결과값이 똑같다.
즉 ! "A번 Index부터 B번 Index까지 +a 를 하고 싶을 때, A번 Index에 + a를 , B + 1번 Index에 -a 연산을 한 후에, 누적합 계산"을 진행하게 되면 하나하나 탐색을 하지 않아도 된다는 것이다. 그럼 이를 이제 우리 문제에 맞게 2차원 배열에서 적용시켜보자.

위와 같은 맵이 주어졌다고 했을 때, "(0 , 0)부터 (2 , 2)까지 모두 + 2 씩 시키세요" 라는 명령어가 떨어졌다고 가정해보자.
똑같이 일단 모든 좌표가 0으로 초기화 되어 있는 새로운 맵을 만들어보자.

2차원 배열도 1차원 배열과 똑같다. 다만, 행에 대해서도 계산을 해줘야 하고 열에 대해서도 계산을 해줘야 하는, 계산을 2번 해야 한다는 것만 다를 뿐, 1차원 배열과 똑같다고 생각을 하면 된다.
그럼 행의 기준에서부터 생각을 해보자.
0 행에서는 어떻게 될까 ?? 0행만 바라본다면 1차원 배열과 똑같기 때문에 다음과 같이 될 것이다.
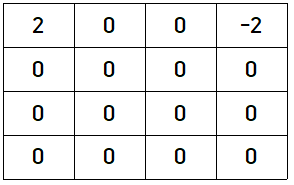
위와 같이 1차원 배열에서와 똑같이 될 것이다. 그런데 이게 0행에서만 일어나면 안된다. 1행, 2행에 대해서도 일어나야 한다.
마찬가지로 1행, 2행에서도 똑같이 적용해보면 다음과 같다.

그럼 행에 대해서는 모두 적용을 시켰다. 이번에는 열에 대해서도 적용을 시켜보자. 이해를 편하게 돕기 위해서 위의 그림은 "행을 위한 그림" 이였다고 생각하고 잊어버리자. 다시 새로운 0으로 초기화된 맵을 가져와서 열에 대해서 계산을 해보자.
열에 대해서도 똑같이 적용하면 다음과 같이 결과가 나오게 될 것이다.
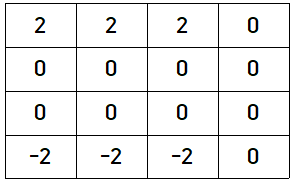
그럼 지금부터는 이걸 하나로 합치게 되면 다음과 같이 그림을 그려볼 수가 있다.

위의 그림이 이해가 안될 수도 있으니, 먼저 행에 대해서 누적합을 구해보겠다.
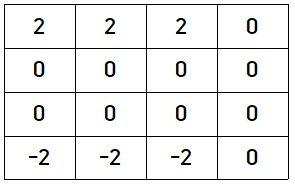
그리고 열에 대해서 누적합을 구해보자.

이와 같이 (0 , 0)과 (2 , 2) 까지만 + 2씩 된 모습을 확인을 할 수가 있다.

정리를 해보면 다음과 같다.
"(x , y)부터 (xx , yy) 까지 + a 를 시키세요" 라는 명령이 주어졌다면,
(x , y) + a
(x , yy + 1) - a
(xx + 1 , y) - a
(xx + 1 , yy + 1) + a
위와 같이 4개의 좌표에 대해서 값을 갱신해 준 후에 누적합을 구하게 되면 (x , y) ~ (xx , yy)까지의 변경된 값을 구할 수가 있다.
누적합을 구할 때에는 위에서도 언급했듯이 행에 대해서 한번, 열에 대해서 한번 총 2번을 계산해 주어야 한다.
누적합을 구했다면, 원본의 맵과 좌표별로 더해서 변화량을 구하게 되면 최종적으로 변화된 값을 원본 맵에서 확인을 할 수가 있다.
이 방법을 사용했을 때 시간복잡도를 계산해보면 다음과 같다.
(x , y) ~ (xx , yy)가 주어졌을 때,
(x , y) + a , (x , yy + 1) - a , (xx + 1 , y) - a , (xx + 1 , yy + 1) + a 이렇게 4개의 좌표 값을 바꾸는데 O(1) 이 걸리게 되고 최종적으로 행에 대한 누적합 1000 * 1000 , 열에 대한 누적합 1000 * 1000 , 원본 맵과 합치는 과정 1000 * 1000 만큼, 3 * 1000 * 1000 이 걸리게 된다. 따라서 이러한 방법으로 문제를 해결할 수 있다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
#include <string>
#include <vector>
using namespace std;
int accSum[1010][1010];
void calculateAccSum(vector<vector<int>> board, vector<vector<int>> skills) {
for (auto skill : skills) {
int type = skill[0];
int x = skill[1];
int y = skill[2];
int xx = skill[3];
int yy = skill[4];
int degree = skill[5];
degree = type == 1 ? degree * -1 : degree;
accSum[x][y] += degree;
accSum[xx + 1][yy + 1] += degree;
accSum[x][yy + 1] -= degree;
accSum[xx + 1][y] -= degree;
}
for (int i = 0; i <= board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
accSum[i][j + 1] += accSum[i][j];
}
}
for (int j = 0; j <= board[0].size(); j++) {
for (int i = 0; i < board.size(); i++) {
accSum[i + 1][j] += accSum[i][j];
}
}
}
int findAnswer(vector<vector<int>> board) {
int answer = 0;
for (int i = 0; i <board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
if (board[i][j] + accSum[i][j] > 0) {
answer++;
}
}
}
return answer;
}
int solution(vector<vector<int>> board, vector<vector<int>> skill) {
int answer = 0;
calculateAccSum(board, skill);
answer = findAnswer(board);
return answer;
}
|
cs |
'[ Programmers Code ] > # PG - Level3' 카테고리의 다른 글
| [ 프로그래머스 양과늑대 (Lv3) ] (C++) (12) | 2022.03.12 |
|---|---|
| [ 프로그래머스 표 편집 (Lv3) ] (C++) (4) | 2021.07.16 |
| [ 프로그래머스 매칭점수 (Lv3) ] (C++) (0) | 2021.07.06 |
| [ 프로그래머스 자물쇠와 열쇠 (Lv3) ] (C++) (1) | 2021.07.04 |
| [ 프로그래머스 다단계 칫솔 판매 (Lv3) ] (C++) (2) | 2021.07.03 |