프로그래머스의 표 편집(Lv3) 문제이다.
[ 문제풀이 ]
문제에서 주어진 연산에 맞게 진행했을 때, 최종적으로 살아있는 행과 삭제된 행에 대해서 출력을 해야 하는 문제이다.
본 문제는, 정확성 테스트와 효율성 테스트가 나눠져 있는 문제이다.
먼저, 쉽게 접근할 수 있는 방법부터 시작해서, 효율성테스트까지 해결할 수 있는 방법까지 단계별로 이야기를 해보자.
#1. 매우 간단한 접근
이 문제를 정말 쉽게 접근한다면 다음과 같은 방법을 이용할 수 있을 것이다.
주어진 크기에 맞는 배열을 만들어 보는 것이다. 또한, 특정 행이 살아있는지 죽어있는지를 표현해놓은 배열을 만들어 보는 것이다.
예를 들어서, 행이 5개가 존재하는 표를 배열로 표현해보면 [ 0 , 1 , 2 , 3 , 4 ] 가 될 것이고, 특정 행이 삭제되었는지 아닌지를 표시해놓은 배열을 표현해보면 [ true , true , true , true , true ] 이런식으로 표현을 할 수 있을 것이다.
초기에는 모든 행이 삭제되지 않았기에 모두 'true' 로 표시를 해 주었다.
그리고, 예를 들어서 2번행이 삭제되었다면, 이를 [ true , true , false , true , true ] 이런식으로 표현을 하는 것이다.
또한, 행을 움직여야하는 'U' 혹은 'D' 명령어에 대해서는, 움직일 칸수만큼 움직여보면서, 해당 행이 살아잇는지 죽어있는지를 계산하면서 움직인다면 충분히 문제를 해결할 수 있을 것이다.
정확성 테스트에서는 이렇게 구현을 하더라도 충분히 가능할 것이다.
전체 표의 크기가 1,000 이고 주어진 명령어의 갯수가 1,000개 이니 극단적인 상황을 한번 가정해보자.
표가 1,000개의 행을 가지고 있는데, 이 때 1번 행부터 998번행까지 모두 삭제되었다고 가정해보자.
그럼 결과적으로 0번행과 999번행 2개의 행만 살아있을 것이다.
그리고 현재 가르키고 있는 행이 0번행이라고 가정해보자. 여기서, 'D 1'이라는 명령어가 주어졌다고 생각해보자.
우리는 위에서 진행한대로 0번행에서 1칸만 올리면 되는데, 사실 998번행까지 모두 탐색을 해볼 것이다.
탐색을 하더라도 모두 삭제된 행이라고 표시가 되어 있기 때문에 결국 1 ~ 998번 행까지 모두 탐색을 한 후에 999번행으로 도달하게 될 것이다. 정확성 테스트에서는 크기가 그리 크지 않기 때문에 충분히 가능할 수도 있지만, 효율성 테스트에서는 문제가 발생하게 된다.
효율성 테스트에서는 주어지는 표의 크기가 백만이 되어버리기 때문에 위와 같이 배열을 이용해서 구현을 하게 되면 너무 많은 시간이 소요되어버리기 때문에 다른 접근 방법이 필요하다. 지금부터는 다른 방법에 대해서 이야기를 해보자.
#2. Linked List
본인은 이 문제를 배열이 아닌, 링크드 리스트를 이용해서 접근해 보았다.
링크드 리스트는 배열과 다르게 삽입 삭제에 대해서 훨씬 더 큰 강점을 가진 자료구조이다.
포인터를 이용해서 노드 간의 연결관계를 표현하기 때문에, 삽입 삭제 시 이 연결관계에 대한 설정만 다시 해주면 되기 때문에 훨씬 더 간편하게 구현할 수 있다.
이 문제 같은 경우에는, 하나의 노드에서 앞으로도 뒤로도 움직일 수 있어야 하기 때문에(U , D명령어) 양방향 링크드 리스트를 구현하였다.
사실, STL에서 제공하는'list'를 통해서 구현을 해보려고 했는데, 본인이 생각한대로 잘 되지 않아서 본인은 직접 링크드리스트를 구현하였다. 지금부터는 링크드리스트에 대해서 구체적으로 이야기를 해보자.
링크드리스트는 이 리스트를 이루고 있는 여러 개의 노드들의 연결관계로 구현을 할 수가 있다.
즉 ! 우리가 구현해야 할 내용은 링크드리스트와 해당 링크드리스트를 구현하고 있는 Node들을 구현하는 것으로 나눠볼 수가 있다.
먼저, Node를 구현하는 과정을 한번 생각해보자.
Node가 가지고 있어야 할 데이터는 뭐가 있어야 할지에 대해서 생각을 해보자.
1. 해당 Node가 가지고 있는 행의 번호 정보를 가지고 있어야 한다.
- 이 부분은 최종적으로 정답을 도출하는 과정에서 필요한 부분이다. 이 데이터를 활용하는 부분은 아래쪽에서
최종적으로 정답을 도출할 때 더욱 구체적으로 이야기를 해보자.
2. 해당 Node의 이전 Node에 대한 정보를 가지고 있어야 한다.
- 양방향 링크드 리스트를 구현할 것이기 때문에, 현재 Node의 이전 Node와도 연결관계가 필요하다.
따라서, 해당 Node의 이전 Node에 대한 정보 또한 필요하다.
3. 해당 Node의 다음 Node에 대한 정보를 가지고 있어야 한다.
- 이 또한, 양방향 링크드리스트를 구현할 것이기 때문에 필요한 정보이다.
본인은 위의 3가지 정보들을 가진 Node를 구조체로 표현해 주었다. 코드로 나타내면 다음과 같다.
struct NODE
{
int Data;
NODE *Prev;
NODE *Next;
NODE(int D)
{
Data = D;
Prev = NULL;
Next = NULL;
}
};
그렇다면, 이제는 이 Node들로 이루어진 링크드 리스트를 구현해보자.
링크드리스트를 구현할 때에는, Head Node와 Tail Node에 대한 정보만 관리할 수 있도록 구현해 주었다.
코드로 나타내면 다음과 같다.
struct LINKEDLIST
{
NODE *Head;
NODE *Tail;
LINKEDLIST() : Head(NULL), Tail(NULL) {}
};
#3. 삭제
이제 링크드리스트에서 진행해야 하는 여러가지 과정에 대해서 구체적으로 이야기를 해보자.
링크드리스트에서 작업을 진행할 때에는 항상 딱 3가지 경우에 대해서만 생각을 해주면 된다.
1. Head Node인 경우
2. Tail Node인 경우
3. Head도 Tail도 아닌 경우
위와 같이 3가지 경우만 생각을 해주면 된다. 예시를 통해서 위의 3가지 경우에 대해서 살펴보자.
만약, 5개의 행이 있는 상태를 링크드 리스트의 상태로 표현해보면 다음과 같을 것이다.

1. Head Node를 삭제하는 경우

Head Node를 삭제하는 경우에 대해서 살펴보자. 위의 그림에서 Head Node를 삭제한다면 아마 다음과 같은 그림이 될 것이다.

Head Node를 삭제하게 되면, 링크드리스트의 Head Node가 바껴 버리게 된다.
또한, 1번 Node의 Prev값, 즉, 1번 Node의 이전 노드에 대한 정보가 사라져 버리게 된다.
1번 Node는 다르게 표현해보면, 0번 Node의 Next Node라고 표현할 수가 있다. 또 다르게 표현해본다면,
Head의 Next Node라고도 표현할 수 있다.
즉 ! Head의 Next Node의 Prev값이 NULL 이 되어버린다.
[ Head Node 를 삭제 시 ]
# Linked List의 Head Node가 Head Node의 Next Node로 바뀌게 된다.
# Head Node의 Next의 Prev Node가 NULL이 되어버린다.
2. Tail Node를 삭제하는 경우

위의 그림에서, 현재 Node 즉, Tail Node를 삭제하게 되면 다음과 같아질 것이다.

Tail Node를 삭제하게 되면, 링크드 리스트의 Tail Node가 바뀌게 될 것이다.
또한, 3번 Node의 Next값, 즉, 3번 Node의 Next Node에 대한 정보가 사라지게 된다.
3번 Node는 다르게 표현해보면, 4번 Node의 Prev Node가 되고, 또 다르게 표현해보면, Tail Node의 Prev Node라고도 표현할 수 있다. 즉 ! Tail Node의 Prev의 Next값이 NULL이 된다.
[ Tail Node 를 삭제 시 ]
# Linked List의 Tail Node가 Tail Node의 Prev Node 로 바뀌게 된다.
# Tail Node의 Prev의 Next Node가 NULL이 되어버린다.
3. 가운데 있는 Node를 삭제 시

그리고 현재 가르키고 있는 지점은 '2번' Node가 있는 빨간색 점이 있는 곳이라고 생각을 해보자.
이 때, 2번 Node를 삭제한다고 생각을 해보자. 그럼 삭제하고 난 뒤의 결과를 본다면 다음과 같을 것이다.

1번 Node의 Next가 3번 Node가 되고, 3번 Node의 Prev Node가 1번 Node가 된다.
1번 Node는 다시 말하면, 현재 삭제하려는 Node의 Prev Node이고, 3번 Node는 현재 삭제하려는 Node의 Next Node이다. 즉 ! 현재 Node의 Prev Node의 Next 값이 현재 Node의 Next 값이 되어버리고, 현재 Node의 Next Node의 Prev값이 현재 Node의 Prev 값이 되어버리게 된다.
말이 되게 복잡해 보이지만 하나하나 따라 가다보면 무슨 말인지 이해가 될 것이다.
[ 가운데 Node를 삭제 시 ]
# 삭제하려는 Node를 'A' 라고 표현해보자.
# A의 Prev Node의 Next는 A의 Next가 된다.
# A의 Next Node의 Prev는 A의 Prev가 된다.
이를 통합해서 코드로 나타내면 다음과 같다.
stack<NODE*> Delete;
NODE* LINKEDLIST::Erase(NODE *Node)
{
Delete.push(Node);
if (Node == Head)
{
Head = Node->Next;
Node->Next->Prev = NULL;
return Node->Next;
}
else if (Node == Tail)
{
Tail = Node->Prev;
Node->Prev->Next = NULL;
return Node->Prev;
}
else
{
Node->Prev->Next = Node->Next;
Node->Next->Prev = Node->Prev;
return Node->Next;
}
}본인은, 삭제 연산을 구현함과 동시에 특정 Node를 return 해주도록 구현하였는데, 이 return해주는 Node가 문제에서 제시한 규칙을 따라주었다.
Head Node와 중간에 있는 Node를 삭제할 때에는 현재 Node의 Next Node를 return해주었으며, Tail Node를 삭제할 때에는 Next Node가 존재하지 않으므로 Prev Node를 return 해 주었다.
그리고 ! 삭제와는 연관이 없지만, 이 문제에서는 "복구하는 과정" 이 필요하다. 명령어 'Z' 때문에 삭제한 Node에 대한 정보를 가지고 있어야 한다. 또한, 복구를 할 때에는 가장 최근에 삭제된 행들에 대해서 순차적으로 복구를 시켜야 하기 때문에 본인은 이 과정을 위해서 stack을 사용해 주었다.
위의 코드에서도 NODE*를 자료형으로 가지는 stack을 생성해 주었다. 그리고 삭제되는 Node를 stack에 삽입해 주었다.
#4. 복구
이제 명령어 'Z'를 위한 복구 과정을 생각해보자. 먼저, 복구를 위해 저장해놓은 데이터는 #3 마지막 과정에서 이야기한 Stack에 저장되어 있을 것이다.
본격적인 복구를 시작하기 전에, Stack에 저장되어 있는 데이터에 대해서 이야기를 해보자.
우리는 삭제를 할 때, 해당 Node 그 자체를 Stack에 저장해 주었다.
한 가지 예를 들어보자.

#3에서 가운데에 있는 Node를 삭제할 때 사용했던 그림이다. 마찬가지로 2번 Node에 대한 정보를 Stack에 담았다고 가정해보자. 삭제한 후 우리는 리스트를 다음과 같이 만들어 주었다.

하지만 여기서 중요한 것이 있다. 우리는 2번 Node를 그대로 Stack에 저장해 주었기 때문에, Stack에서 가져온 Node에는 2번 Node의 정보가 그대로 담겨져 있다는 것이다.
즉 ! 2번 Node의 Prev Node가 1번 Node라는 정보와, 2번 Node의 Next Node가 3번 Node라는 정보 또한 가지고 있다는 것이다. 이를 이용해서 손쉽게 복구 작업을 진행할 수 있다.
복구 작업도 크게 3가지로 나눠서 생각을 하면된다. Head, Tail, 그게 아닌 상황.
1. Head Node를 복구 시
복구하려는 Node가 List에서 Head Node 였다는 것을 어떻게 확인할 수 있을까 ??
바로 Head Node는 LinkedList에서 유일하게 Prev Node가 NULL 인 Node이다. 이를 이용해서, Head Node라는 것을 알 수 있다. 또한, 복구하는 순간, 현재 LinkedList의 Head Node의 Prev 값이 NULL 값이 아닌, 복구하는 Node가 될 것이다. 동시에, LinkedList의 Head Node가 바뀌게 될 것이다.
[ Head Node를 복구 시 ]
# 복구 하려는 Node를 'A' 라고 표현해보자.
# 'A'의 Prev 값이 NULL 임을 통해서 Head Node 라는 것을 알 수 있다.
# Linked List의 Head의 Prev 값이 NULL에서 A로 바뀌게 된다.
# Linked List의 Head가 A로 바뀌게 된다.
2. Tail Node를 복구 시
Tail Node는 LinkedList에서 유일하게 Next Node가 NULL인 Node이다. 이를 이용해서, Tail Node라는 것을 알 수 있다. 또한, 복구하는 순간, 현재 LinkedList의 Tail Node의 Next 값이 NULL 값이 아닌, 복구하는 Node가 될 것이다.
동시에, LinkedList의 Tail Node가 바뀌게 될 것이다.
[ Tail Node를 복구 시 ]
# 복구 하려는 Node를 'A'라고 표현해보자.
# A의 Next 값이 NULL임을 통해서 Tail Node라는 것을 알 수 있다.
# Linked List의 Tail의 Next값이 NULL에서 A로 바뀌게 된다.
# Linked List의 Tail이 A로 바뀌게 된다.
3. Head, Tail이 아닌 Node 복구 시
복구하려는 Node를 'A' Node라고 표현해보자.
즉, 이런상황일 것이다.
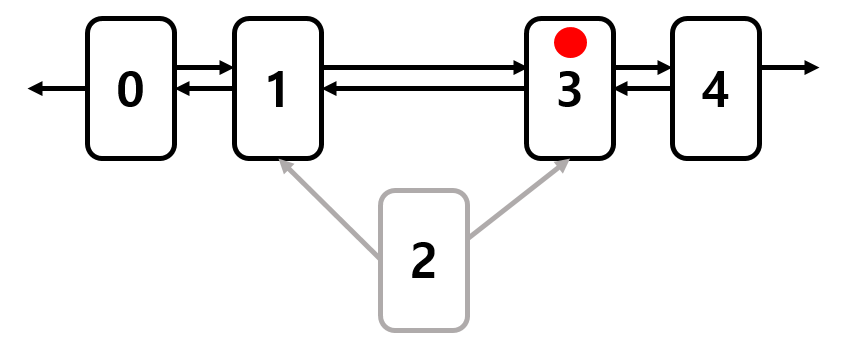
이 상태에서, 2번 Node를 복구하는 과정을 보자. 복구를 하게 되면 2번 Node의 Prev의 Next 값은 2번 Node가 될 것이다. 또한, 2번 Node의 Next의 Prev 값은 2번 Node가 될 것이다.
[ 가운데 Node를 복구 시 ]
# 복구하려는 Node를 'A'라고 표현해보자.
# A의 Prev의 Next는 A가 될 것이다.
# A의 Next의 Prev는 A가 될 것이다.
위와 같은 과정들을 통해서, 삭제와 복구를 진행할 수 있다. 이 글에서 단순히 가르키는 포인터를 옮기는 U와 D 명령어에 대해서는 언급하지 않았는데, 이 명령어들은 단순하게 for문을 통해서 Prev 혹은 Next로 옮겨 주는 단순한 과정이라서 최종 소스코드에서 참고하도록 하자.
#5. 정답도출
이제 최종적으로 정답을 도출해보자. 본인은 일단 초기에 주어진 표의 크기만큼을 길이로 가지는 문자열을 하나 만들어 주었다. 그리고 해당 문자열을 'O'로 가득 채워 주었다.
만약, 표의 크기가 '5'인 케이스였다면, Result = "OOOOO" 로 채워주었다.
그런데 ! 중간에 삭제된 케이스들이 있을 수 있다. 이 케이스들을 어떻게 X로 바꿀 수 있을까 ??
삭제된 케이스들은 #3에서 이야기했던 Stack에 아직 저장되어 있을 것이다. Stack에는 Node 그 자체를 저장했으므로 해당 Node가 가지고 있는 정보들을 가져올 수 있다고 했다. 그런데 ! Node에는 "행의 번호" 또한 저장이 되어 있다.
#2에서 했던 이야기인데, 바로 이 부분에서 저장된 행의 번호가 사용되어 진다.
행의 번호는 곧 최종 문자열에서의 Index번호와 동일하다.
예를 들어서, Stack에 행의 번호가 '1'인 Node가 저장되어 있다면, 이는 최종 문자열에서 1번 Index가 'X'가 된다는 것을 의미한다. 즉, Result = "OXOOO" 가 될 것이다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
|
#include <string>
#include <vector>
#include <stack>
using namespace std;
struct NODE
{
int Data;
NODE *Prev;
NODE *Next;
NODE(int D)
{
Data = D;
Prev = NULL;
Next = NULL;
}
};
struct LINKEDLIST
{
NODE *Head;
NODE *Tail;
LINKEDLIST() : Head(NULL), Tail(NULL) {}
void Insert(int _Data);
NODE* Erase(NODE *Node);
void Restore(NODE *Node);
};
void LINKEDLIST::Insert(int _Data)
{
if (Head == NULL)
{
NODE *NewNode = new NODE(_Data);
Head = NewNode;
Tail = NewNode;
}
else
{
NODE *NewNode = new NODE(_Data);
NewNode->Prev = Tail;
Tail->Next = NewNode;
Tail = Tail->Next;
}
}
NODE* LINKEDLIST::Erase(NODE *Node)
{
if (Node == Head)
{
Head = Node->Next;
Node->Next->Prev = NULL;
return Node->Next;
}
else if (Node == Tail)
{
Tail = Node->Prev;
Node->Prev->Next = NULL;
return Node->Prev;
}
else
{
Node->Prev->Next = Node->Next;
Node->Next->Prev = Node->Prev;
return Node->Next;
}
}
void LINKEDLIST::Restore(NODE *Node)
{
if (Node->Prev == NULL)
{
Head = Node;
Node->Next->Prev = Node;
}
else if (Node->Next == NULL)
{
Tail = Node;
Node->Prev->Next = Node;
}
else
{
Node->Prev->Next = Node;
Node->Next->Prev = Node;
}
}
stack<NODE*> Delete;
LINKEDLIST *List;
void Make_LinkedList(int N)
{
List = new LINKEDLIST();
for (int i = 0; i < N; i++) List->Insert(i);
}
string Solve(int N, int K, vector<string> Cmd)
{
NODE *Iter = List->Head;
for (int i = 0; i < K; i++) Iter = Iter->Next;
for (int i = 0; i < Cmd.size(); i++)
{
string Str = Cmd[i];
if (Str[0] == 'U')
{
string SX = Str.substr(2);
int X = stoi(SX);
for (int i = 0; i < X; i++) Iter = Iter->Prev;
}
else if (Str[0] == 'D')
{
string SX = Str.substr(2);
int X = stoi(SX);
for (int i = 0; i < X; i++) Iter = Iter->Next;
}
else if (Str[0] == 'C')
{
Delete.push(Iter);
Iter = List->Erase(Iter);
}
else
{
NODE *Z = Delete.top();
Delete.pop();
List->Restore(Z);
}
}
string Result = "";
for (int i = 0; i < N; i++) Result += 'O';
while (Delete.empty() == false)
{
NODE *Temp = Delete.top();
Delete.pop();
int Idx = Temp->Data;
Result[Idx] = 'X';
}
return Result;
}
string solution(int n, int k, vector<string> cmd)
{
string answer = "";
Make_LinkedList(n);
answer = Solve(n, k, cmd);
return answer;
}
|
cs |
'[ Programmers Code ] > # PG - Level3' 카테고리의 다른 글
| [ 프로그래머스 파괴되지 않은 건물 (Lv3) ] (C++) (4) | 2022.03.13 |
|---|---|
| [ 프로그래머스 양과늑대 (Lv3) ] (C++) (12) | 2022.03.12 |
| [ 프로그래머스 매칭점수 (Lv3) ] (C++) (0) | 2021.07.06 |
| [ 프로그래머스 자물쇠와 열쇠 (Lv3) ] (C++) (1) | 2021.07.04 |
| [ 프로그래머스 다단계 칫솔 판매 (Lv3) ] (C++) (2) | 2021.07.03 |