프로그래머스의 시험장 나누기(Lv5) 문제이다.
[ 문제풀이 ]
주어진 이진트리를 K개의 서브트리로 나눴을 때, 인원이 가장 많은 그룹의 인원의 최소값을 구해야 하는 문제이다.
전체적인 직관적인 접근방법부터 구체적인 풀이과정 그리고 정답을 도출하는 과정까지 진행해보자.
#1. 접근방법
지금부터 우리는 이 문제를 보고 그대로 접근하는 것이 아니라 한번 역으로 생각을 해볼 것이다.
주어진 이진트리를 K개의 서브트리로 나누고 난 후에, 각 서브트리가 가지는 인원의 합 중 최댓값을 최소가 되도록 만들어야 하는 문제이니까, 이를 역으로 한번 생각을 해보는 것이다.
K개의 서브트리로 나누고 난 후에, 인원의 수를 카운트 하는 방식이 아닌 인원의 수를 카운트 하면서 K개의 서브트리로 나눌 수 있는지로 생각을 해보는 것이다.
더 쉽게 이야기 해보자면, 각 서브트리에 들어가는 인원의 합이 'A명' 이하가 되도록 트리를 나누고 난 후에, 나눈 트리의 갯수가 K개 이하인지를 확인해 보는 것이다. 지금부터 편하게 "우리가 설정할 각 서브트리에 들어가는 인원의 합을 'A'"라고 표현하겠다. 즉, 우리는 지금부터 이 'A'의 값을 우리가 임의적으로 설정해주고, 모든 서브트리의 합이 A명 이하가 되도록 여러 개의 서브트리로 나눴을 때, 이 나눈 트리의 갯수가 K개 이하인지를 확인해 볼 것이다.
(여기서 왜 정확하게 K개로 나누는 것이 아닌, K개 이하인지를 확인하는지에 대해서는 밑에서 더욱 구체적으로 이야기 해보도록 하자.)
다시 본론으로 돌아와서, 우리는 문제를 역으로 접근을 할 것이다. 서브트리를 K개로 나눌 수 있는 모든 경우를 구한 후에, 각 서브트리의 합을 구해서 최대인원의 최소값을 구하는 것이 아닌, 트리를 인원의 합이 A명 이하가 되도록 여러개의 서브트리로 나눈 후에, 나눠진 서브트리의 갯수가 K개 이하인지를 확인할 것이다.
그렇다면, 어떻게 이를 코드로써 표현을 할 수 있을까 ??
가장 쉬운 방법이 하나가 있다. 우리가 설정해줄 "트리를 합이 A명 이하인 여러개의 서브트리가 되도록 만들기" 과정에서 필요한 이 'A'의 값을 모두 탐색해 보는 방법이 있다.
저 A의 값을 1부터 계속해서 차근차근 늘려가면서 탐색을 해본다면 결국 정답이 나올 것이다.
그렇다면, A값의 범위에 대해서 생각을 해보자.
정확성 테스트에서 보게되면, 우리에게 주어진 solution 함수의 매개변수로 주어지는 num 변수의 길이, 즉, 주어진 트리의 노드의 갯수이자 시험장의 갯수가 20이라고 되어 있다. 그리고, num의 각 원소는 최소 1에서 최대 10,000 의 값을 가질 수 있다고 되어 있다.
즉, 최악의 경우 최대 20개의 시험장이 주어질 수 있고, 각 시험장에는 10,000명씩 들어간 경우 또한 발생할 수 있다는 것이다. 그럼, 우리는 A값의 범위를 어떻게 설정할 수 있을까 ?
일단, 최소값은 1명일 것이다. 모든 원소가 최소 1명은 들어있기 때문에 우리는 서브트리의 합이 1이 되도록 탐색을 진행해볼 수도 있을 것이다. 그렇다면 최댓값은 ? 20개의 시험장에 10,000명이 들어간 경우, 즉, 200,000이 될 것이다.
우리는 1 <= A <= 200,000 에 대한 모든 A에 대해서 탐색을 진행한다면 정답을 구할 수 있을 것이다.
다시한번 이야기해보면, 우리는 "주어진 트리를 여러 개의 서브트리로 나눌 것인데, 이 때 각각의 서브트리는 1 ~ 200,000명 이하가 되도록 서브트리를 나눠볼 것입니다. 이 때, 서브트리를 K개 이하로 나눌 수 있을까요 ?" 에 대해서 문제를 해결하는 것이다.
1 ~ 20만이라면 완전탐색을 통해서도 문제를 해결할 수 있을 것이다. 하지만 ! 이는 언제까지나 "정확성 테스트"에서만 해당되는 이야기이다. 본 문제는 효율성 테스트 까지 가지고 있으며, 효율성 테스트에서는 시험장의 수, 즉, num의 크기가 10,000 까지 주어질 수 있다.
그렇다면 이 경우에는 A의 범위가 1 <= A <= 10,000 * 10,000 이 될 것이다. 약 1억번의 연산을 진행해야 할 것이고, 이 외에 트리를 나누는 과정 이런 과정까지 포함한다면 굉장히 오랜 시간이 걸리게 될 것이다.
따라서, 이렇게 완전탐색으로 진행을 한다면 정답을 도출하기에 조금 부담스러운 부분이 존재한다.
지금부터는 이 부담스러운 부분을 어떻게 하면 효율적인 방법으로 바꿀 수 있는지에 대해서 이야기를 해 볼 것이다.
우리가 지금까지 한 이야기를 통해서, 우리는 "주어진 트리를 K개로 나눈 후, 각 서브트리에 있는 인원의 합을 구해서 최대인원의 최소값을 구하기"가 아닌, "주어진 트리를, 정해놓은 인원의 합 A 이하가 되도록 서브트리를 나눈 후, 나눈 서브트리의 갯수가 K개 이하가 되는지" 로 문제를 접근한다는 것만 알고 다음 단계로 넘어가보자.
#2. 이분 탐색을 이용한 접근
#1에서 이야기했듯이, A의 값을 완전탐색으로 탐색을 하기에는 너무 오랜 시간이 걸리게 된다.
그래서 본인은 이분 탐색으로 탐색하는 부분을 접근해 보았다. 이분탐색으로 진행을 하게 되면, O(log2(1억)) 의 시간에 답을 도출할 수 있기 때문에 완전탐색으로 하는 것 보다 훨씬 빠르게 탐색을 진행할 수 있다.
탐색을 하는 부분에 대한 간략한 코드는 다음과 같다.
int Binary_Search(int K)
{
/* K = 나눌 그룹의 수. */
/* 그리고 최대 몇 명 이하로 그룹을 묶을하지 정할 값이 필요하다. = Binary_Search의 Mid 값. */
int Result = 987654321;
int Start = 1;
int End = 10000 * 10000;
while (Start <= End)
{
int Mid = (Start + End) / 2;
if (Search(K, Mid) == true)
{
End = Mid - 1;
Result = Min(Result, Mid);
}
else Start = Mid + 1;
}
return Result;
}당연 초기 범위는 1 ~ 1억일 것이다. 따라서 위와 같이 Start 와 End의 값을 설정해 주고 탐색을 진행해 주었다.
지금부터는 탐색을 진행하는 구체적인 과정에 대해서 알아보자.
#3. 노드간의 관계 설정
먼저 탐색을 진행하기 전에 노드간의 관계를 설정하는 부분에 대해서부터 이야기를 해보자.
이진트리로 주어진다고 했으니, 당연히 모든 노드들에 대해서 부모 - 자식 관계가 성립할 것이다.
따라서, 노드들의 부모와 자식간의 관계를 설정해 주었다.
또한 ! 탐색을 하기 위해서 트리의 가장 핵심 노드인 'Root 노드' 또한 찾아 주었다.
Root 노드는 유일하게 "누군가의 자식이 아닌 노드" 라는 것을 이용해서 Root 노드를 찾아 주었다.
코드로 나타내면 다음과 같다.
bool Is_Child[MAX];
int Left_Child[MAX];
int Right_Child[MAX];
void Make_Binary_Tree(vector<vector<int>> Link)
{
fill(Left_Child, Left_Child + MAX, -1);
fill(Right_Child, Right_Child + MAX, -1);
for (int i = 0; i < Link.size(); i++)
{
int Left = Link[i][0];
int Right = Link[i][1];
if (Left != -1)
{
Left_Child[i] = Left;
Is_Child[Left] = true;
}
if (Right != -1)
{
Right_Child[i] = Right;
Is_Child[Right] = true;
}
}
for (int i = 0; i < Num.size(); i++)
{
if (Is_Child[i] == false)
{
Root = i;
break;
}
}
}Is_Child[] 변수는 해당 노드가 다른 노드의 자식 노드인지 아닌지를 판단해 주기 위해 선언한 배열이다.
Is_Child[A] = true 라는 것은, "노드 A는 누군가의 자식 Node 입니다." 를 의미한다. 즉 ! Root 노드가 아니라는 것을 의미한다. 반대로, Root노드만 Is_Child[]의 값이 false일 것이다. Root노드는 누군가의 자식 Node가 될 수 없기 때문이다.
Left_Child[A] = B의 의미는, "A의 왼쪽 자식 노드는 B입니다."를 의미한다.
Right_Child[A] = B의 의미는, "A의 오른쪽 자식 노드는 B입니다."를 의미한다.
#4. 탐색 과정
이제 본격적으로 탐색하는 과정에 대해서 알아보자.
먼저 #1과 #2에서 했던 이야기들을 다시한번 정리해보자.
우리는, 주어진 트리를 K개의 서브트리로 나눈 후, 각 서브트리의 인원 수를 Count한 후에 최대인원의 값 중 최소값을 찾는 것이 아니라, 주어진 트리를 여러 개의 서브트리로 나눌 건데, 이 때 각 서브트리의 인원 수가 A명 이하가 되도록 나눈 후에, 서브트리가 몇 개 발생했는지를 체크해봄으로써 문제를 해결할 거라고 했었다.
즉 ! 우리는 지금부터, "특정 노드를 서브트리의 Root Node로 삼았을 때, 해당 서브트리의 인원의 총 합이 A이하가 되도록 만드는 과정" 을 진행할 것이다.
탐색을 할 때에는 다음과 같은 여러 가지 Case들이 발생할 수 있다. 지금부터 편의를 위해서 다음과 같은 용어들을 사용해 볼 것이다.
Cur = 현재 서브트리의 루트노드가 되는 노드를 의미하면서 동시에 해당 노드가 가지고 있는 인원수를 의미한다.
LC = Left_Child로, Cur 의 Left_Child를 의미하면서 동시에 해당 노드가 가지고 있는 인원수를 의미한다.
RC = Right_Child로, Cur의 Right_Child를 의미하면서 동시에 해당 노드가 가지고 있는 인원수를 의미한다.
1. Cur > A
그림으로 나타내면 다음과 같은 상황이다.

우리가 설정해놓은 각 서브트리에 들어갈 인원수가 100명 이하가 되도록 트리를 나누고 싶은데, 이 때 위와 같은 상황인 것이다. Cur = 200 으로, 자식노드를 포함하지 않더라도, Cur만으로도 절대로 인원수가 100명 이하가 되도록 만들 수가 없는 상황이다. 이 경우에는 'A'의 값을 다시 설정해줘야 하고 더 이상의 탐색 또한 필요가 없다.
2. Cur + LC + RC <= A
그림으로 나타내면 다음과 같은 상황이다.

우리가 설정해놓은 각 서브트리에 들어갈 인원수가 100명 이하가 되도록 트리를 나누고 싶은데, 이 떄 위와 같은 상황인 것이다. Cur = 10 , LC = 2 , RC = 3 인 경우이다. 자기자신을 포함해서 모든 자식들을 다 합치더라도 제한된 목표 인원인 100명 이하인 경우이다. 이 경우에는 위의 트리를 더 작은 트리로 나눌 필요가 없게 된다.
즉 ! 이 경우에는 트리를 더 잘게 나눌 필요 없이, 위의 인원수들을 모두 합친 하나의 서브트리를 만들 수 있는 것이다.
3. Cur + LC > A && Cur + RC > A
그림으로 나타내면 다음과 같은 경우이다.

위와 같은 경우를 생각해보자. 우리는 서브트리의 인원이 15명 이하가 되도록 만들고 싶은데, 어느 한쪽의 자식만 포함하게 되더라도 해당 인원을 초과해 버리는 상황이다.
왼쪽 자식만 데려가고 오른쪽 자식과 관계를 끊는다고 해도, 10 + 6 으로 15를 초과해 버리게 되고,
오른쪽 자식만 데려가고 왼쪽 자식과 관계를 끊는다고 해도, 10 + 7 로 15를 초과해 버리게 되는 것이다.
이 경우에는 어쩔 수 없이 어느 하나의 자식도 데려갈 수 없이 모두 연결을 끊어줘야 한다.

위와 같이 끊어야지만, 서브트리의 인원이 모두 15 이하로 만들 수 있게 된다.
이 경우에는, 트리를 나눈 횟수가 '2' 증가하게 된다. 왼쪽 자식과 나누면서 한번, 오른쪽 자식과 나누면서 한번, 총 2번 트리를 나누게 된다.
4. Cur + LC > A
이 경우를 살펴보자.

위와 같은 경우이다. 오른쪽 자식만 합쳤을 때는 제한된 인원 A보다 더 적지만, 왼쪽 자식만 합쳤을 때는 제한된 인원 A를 초과하는 경우이다. 이 경우에는 ? 왼쪽 자식과 관계를 끊고 오른쪽 자식만 데려갈 수가 있다.

즉, 위와 같이 왼쪽 자식만 끊고 오른쪽 자식을 데려간다면 모든 서브트리의 인원수의 합이 A 이하가 되도록 만들 수 있다. 이 경우에는, 트리를 나눈 횟수가 1회 증가하게 된다.
5. Cur + RC > A
4번과 반대되는 경우이다. 이 경우에는 오른쪽 자식과의 관계를 끊고 왼쪽 자식만 데려가게 되면 모든 서브트리의 인원수의 합이 A이하가 되도록 만들 수 있다. 이 경우 또한, 트리를 나눈 횟수가 1회 증가하게 된다.
6. Cur + LC < A && Cur + RC < A
다음과 같은 경우이다.

2개의 자식을 모두 데려가게 되면, 서브트리의 합이 A를 초과해서 둘 다 데려갈 수는 없지만 위에서 이야기했던 4번, 5번 Case와는 다르게 LC를 데려갈 수도 있고, RC를 데려갈 수도 있는 선택권이 있는 상황이라고 볼 수 있다.
4번, 5번 Case의 경우에는 어느 한쪽이 A를 초과해버려서 선택권이 없었지만 이 경우는 선택권이 있는 상황이다.
이 때는, 어느 자식을 데려가는 것이 맞을지에 대해서 생각을 해보자.
우리가 구하고자 하는 값은, "최대인원을 가진 서브트리에서 최솟값" 이다. 즉 ! 결과적으로 우리가 구해야 하는 값은 상대적으로 더 작은 값인 최소값을 구해야 하는 상황이다.
따라서, 위와 같은 선택지가 있는 상황에서는 더 작은 값을 가진 자식 노드를 데려가는 것이 올바른 선택이 되는 것이다.
마찬가지로, 어느 한쪽 자식과는 연결을 끊어야 하기 때문에 트리를 나눈 횟수가 1회 증가하게 된다.
이렇게 총 6가지 경우가 발생할 수 있다. 지금 위의 그림에서는 노드가 3개만 존재하는 아주 극단적인 상황을 예시로 들었지만 실제로는 루트노드부터 위와 같은 탐색이 계속해서 진행된다.
우리가 생각을 해줘야 하는 것은, 중간 중간 트리를 나누는 과정에서 몇 번 나눴는지를 Count 해주는 것이 중요하다.
이 모든 과정들을 재귀를 통해서 진행해 주었다. 코드로 나타내면 다음과 같다.
bool Can_Divide;
int Divide_Cnt;
int DFS(int Cur, int Mid)
{
if (Cur == -1) return 0;
if (Num[Cur] > Mid)
{
Can_Divide = false;
return -1;
}
int LC = DFS(Left_Child[Cur], Mid);
int RC = DFS(Right_Child[Cur], Mid);
if (Can_Divide == false) return 0;
int Case = Find_Case(Num[Cur], LC, RC, Mid);
if (Case == 1) return Num[Cur] + LC + RC;
else if (Case == 2)
{
Divide_Cnt += 2;
return Num[Cur];
}
else if (Case == 3)
{
Divide_Cnt += 1;
return Num[Cur] + RC;
}
else if (Case == 4)
{
Divide_Cnt += 1;
return Num[Cur] + LC;
}
else
{
Divide_Cnt += 1;
return (Num[Cur] + Min(LC, RC));
}
}
bool Search(int K, int Mid)
{
Divide_Cnt = 0;
Can_Divide = true;
DFS(Root, Mid);
if (Divide_Cnt >= K) return false;
if (Can_Divide == false) return false;
return true;
}DFS안에 있는 두 번째 조건문인 Num[Cur] > Mid 라는 조건문이 위에서 이야기한 1번 Case에 해당하는 부분이다. 이 경우에는 하나의 Node만으로도 이미 A를 초과해버리기 때문에 A의 값을 다시 재설정하는 방법밖에 존재하질 않는다.
그리고 LC, RC의 값 또한 DFS를 통해서 LC가 Root Node가 되는 서브트리의 자식들의 상태, RC가 Root Node가 되는 서브트리의 자식들의 상태 또한 모두 받아온 후에 진행하게 된다.
밑에 if - else문에 걸려있는 Case 1 , 2 , 3 , 4 , 5 가 우리가 위에서 이야기 했던 Case 2, 3, 4, 5, 6에 해당하는 구문들이다.
아까도 말했듯이, 우리에게 중요한 것은, 몇 개의 서브트리로 나눴는지가 가장 중요하다. 따라서 ,Search() 함수에서 보게 되면, DFS탐색 후에, 나눈 횟수(본문 : Divide_Cnt)가 K번 이상인지 확인하는 부분이 있다.
그런데 ! 위에서 잠깐 이야기하고 넘어간 부분과 또 한가지 부분에 대해서 이야기를 해보자.
1. Divide_Cnt >= K ?
도대체 왜, 나눈 횟수가 K번일 때에도 false를 return 하는 것일까 ? K개의 서브트리로 만들 수 있다면 나눈 횟수가 K번일 때에도 정확하게 탐색이 된 것이 아닐까 ??
위의 Divide_Cnt 값은 "나눈 횟수"를 의미하기 떄문이다. 즉 ! 이 값은 발생한 서브트리의 갯수를 의미하는 것이 아니다.
하나의 트리에서 1번 나누게 되면, 2개의 서브트리가 발생하게 된다.
하나의 트리에서 2번 나누게 되면, 3개의 서브트리가 발생하게 된다.
하나의 트리에서 K번 나누게 되면, K + 1개의 서브트리가 발생하게 된다.
즉 ! K번 나누게 되면, 결과적으로 K + 1개의 서브트리가 발생했음을 의미하기 때문에 이 또한 잘못된 탐색인 것이다.
2. 왜 K개의 서브트리로 만들지 않았을 때에도 올바르게 탐색이 되었다고 표현할까 ?
한 가지 예를 들어보자.
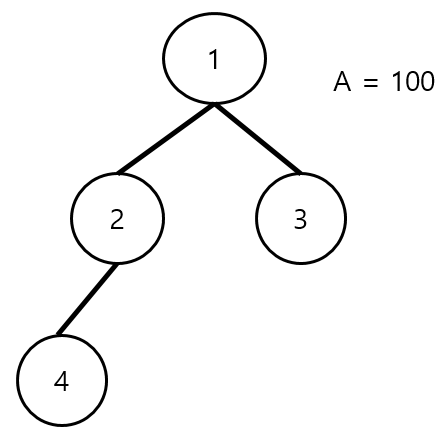
위와 같은 트리가 존재한다. 그리고 우리가 위의 트리를 2개의 서브트리로 만들었을 때, 최대인원의 최소값을 구한다고 가정해보자.
1번을 Root Node로 하면서 모든 자식들을 다 합쳐도 100명 이하로 되기 때문에 굳이 나누지 않아도 될 것이다.
그리고 위의 코드에서 이 상황을 적용해보면, 올바르게 탐색이 되었다는 결론을 도출하게 될 것이다.
그런데 사실 잘못된 경우가 아닐까 ?? 우리는 2개의 서브트리를 만들었을 때, 최대인원의 최소값을 구하고 싶은건데, 위의 경우는 2개의 서브트리를 만들지 않았을 경우이기 때문에 정확한 경우가 아니지 않을까 ??
정확한 경우는 아니라고 보기 어렵다. 단지 이런 경우는 "무의미한 결과값을 가지고 있는 경우" 라고 생각할 수 있다.
왜 그럴까 ??
다시 처음으로 돌아가보자.
우리는 이분탐색을 위해 초기 Left값을 '1', Right값을 '1억' 으로 설정을 하고 Mid의 값을 바꿔가면서 탐색을 진행하였다.
위의 상황에서 이를 적용했을 때, Mid 값이 100이 나온 경우를 생각해보자.
100이 나온 경우, K개 이하(2개 이하)의 서브트리를 만들었고 이 때 최대인원의 최소값은 10으로 측정될 것이다.
하지만, 그 이후에 계속해서 탐색을 진행해서 Mid 값이 '6'이 나온 경우를 살펴보자.
이 경우에는 1번 Node에서 2번 Node로 가는 간선을 잘라버리게 되면 성공적으로 탐색을 끝낼 수가 있다.
그리고 이때 정답은 100에서 6으로 갱신이 될 것이다.
즉 ! K개 미만의 서브트리를 만들어서 탐색을 마쳤을 때에는, 잘못된 탐색은 아니지만 크게 유의미한 결과값을 가지고 있는 것은 아니다. 왜냐하면 K개의 서브트리를 만들게 되면 당연히 결과값에 더 작아지는게 자명한 사실이기 때문이다.
각 노드가 가진 값들은 1이상의 값이고 음수가 존재하지 않는다. 따라서, 더 적은 수의 서브트리를 만들었을 때 결과값이 더 커지는 경우는 없다는 것이다. 반드시 더 작은 결과값만이 존재한다는 것이다.
위의 경우에서도 1개의 서브트리를 만들었을 때의 결과값보다 2개의 서브트리를 만들었을 때 결과값이 더 작듯이, 모든 경우가 위와 같은 상황에 해당한다는 것이다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
|
#include <string>
#include <vector>
#include <algorithm>
#define MAX 10010
using namespace std;
int Root, Divide_Cnt;
bool Can_Divide;
bool Is_Child[MAX];
int Left_Child[MAX];
int Right_Child[MAX];
vector<int> Num;
int Min(int A, int B) { return A < B ? A : B; }
void Make_Binary_Tree(vector<vector<int>> Link)
{
fill(Left_Child, Left_Child + MAX, -1);
fill(Right_Child, Right_Child + MAX, -1);
for (int i = 0; i < Link.size(); i++)
{
int Left = Link[i][0];
int Right = Link[i][1];
if (Left != -1)
{
Left_Child[i] = Left;
Is_Child[Left] = true;
}
if (Right != -1)
{
Right_Child[i] = Right;
Is_Child[Right] = true;
}
}
for (int i = 0; i < Num.size(); i++)
{
if (Is_Child[i] == false)
{
Root = i;
break;
}
}
}
int Find_Case(int Cur, int L, int R, int Mid)
{
if (Cur + L + R <= Mid) return 1;
if (Cur + L > Mid && Cur + R > Mid) return 2;
if (Cur + L > Mid) return 3;
if (Cur + R > Mid) return 4;
return 5;
}
int DFS(int Cur, int Mid)
{
if (Cur == -1) return 0;
if (Num[Cur] > Mid)
{
Can_Divide = false;
return -1;
}
int LC = DFS(Left_Child[Cur], Mid);
int RC = DFS(Right_Child[Cur], Mid);
if (Can_Divide == false) return 0;
int Case = Find_Case(Num[Cur], LC, RC, Mid);
if (Case == 1) return Num[Cur] + LC + RC;
else if (Case == 2)
{
Divide_Cnt += 2;
return Num[Cur];
}
else if (Case == 3)
{
Divide_Cnt += 1;
return Num[Cur] + RC;
}
else if (Case == 4)
{
Divide_Cnt += 1;
return Num[Cur] + LC;
}
else
{
Divide_Cnt += 1;
return (Num[Cur] + Min(LC, RC));
}
}
bool Search(int K, int Mid)
{
Divide_Cnt = 0;
Can_Divide = true;
DFS(Root, Mid);
if (Divide_Cnt >= K) return false;
if (Can_Divide == false) return false;
return true;
}
int Binary_Search(int K)
{
/* K = 나눌 그룹의 수. */
/* 그리고 최대 몇 명 이하로 그룹을 묶을 수 있는 값이 필요하다. = Binary_Search의 Mid 값. */
int Result = 987654321;
int Start = 1;
int End = 10000 * 10000;
while (Start <= End)
{
int Mid = (Start + End) / 2;
if (Search(K, Mid) == true)
{
End = Mid - 1;
Result = Min(Result, Mid);
}
else Start = Mid + 1;
}
return Result;
}
int solution(int k, vector<int> num, vector<vector<int>> links)
{
int answer = 0;
Num = num;
Make_Binary_Tree(links);
answer = Binary_Search(k);
return answer;
}
|
cs |
'[ Programmers Code ] > # PG - Level5' 카테고리의 다른 글
| [ 프로그래머스 방의 개수 (Lv5) ] (C++) (16) | 2020.11.01 |
|---|