백준의 빗물(14719) 문제이다.
[ 문제 바로가기 ]
[ 문제풀이 ]
2차원으로 맵이 하나 주어졌을 때, 해당 맵에서 고일 수 있는 빗물의 총량을 구해야 하는 문제이다.
빗물이 고이는 기본적인 원리부터 정답을 도출하는 과정까지 함께 진행해보자.
#1. 빗물이 고이는 공간과 양
먼저, 빗물은 어느 위치에 어느정도의 양으로 고일 수 있는지 부터 알아보자.
가장 먼저, 제일 왼쪽에 있는 칸을 생각해보자. 쉽게 이해하기 위해서 가로의 길이가 1인 경우를 살펴보자.

위와 같은 상황을 생각해보자. 위의 그림에서는 빗물이 얼마나 고일 수 있을까 ??
'3'만큼 빗물이 고일 수 있을까 ?? 그렇지 않다. 위의 경우 빗물이 고일 수 있는 양은 0이 된다.
즉 ! 주어진 맵에서 가장 왼쪽과 가장 오른쪽은 빗물이 절대로 고일 수 없는 영역이라는 것이다.
따라서 우리는 주어진 맵의 가로길이가 'W'라고 가정했을 때, 빗물이 고일 수 있는 영역인 2 ~ W - 1 까지만 탐색을 해보면 된다. 그렇다면 지금부터 빗물이 얼만큼 고일 수 있는지를 알아보자.
쉽게 이야기하기 위해서 예제 입력1을 가지고 진행해보자. 예제 입력1을 그림으로 표현하면 다음과 같다.

일단 가장 왼쪽과 오른쪽 열은 빗물이 고일 수 없음을 알았으니 2번 열부터 진행을 해보자.
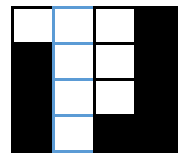
위의 그림에서 파랑색 영역에는 빗물이 얼마나 쌓일 수 있을까 ??
빗물이 고일 수 있는 양은 다음과 같은 조건들에 의해서 결정되어 진다.
1. 해당 열을 제외한, 나머지 열들의 높이에 의해서 결정된다.
2. 나머지 열들은 해당 열을 기준으로 왼쪽에 있는 열, 오른쪽에 있는 열로 나눌 수 있다.
3. 왼쪽에 있는 열들 중에서의 최대높이와 오른쪽에 있는 열들 중에서의 최대높이에 의해 결정된다.
4. 3의 과정에서 구한 최대높이 중, 더 낮은 높이에 의해 결정된다.
5. 4의 과정에서 구한 높이와 현재 열의 높이의 차이 만큼 빗물이 고이게 된다.
2번 열부터 위의 과정에 맞게 진행해보자. 2번 열의 높이 = 0
2. 나머지 열들을 해당 열을 기준으로 왼쪽에 있는 열, 오른쪽에 있는 열로 나눌 수 있다.
- 왼쪽에는 1열 하나만 존재하고, 오른쪽에는 3열 4열 2개가 존재한다.
3. 왼쪽에 있는 열들 중에서의 최대높이와 오른쪽에 있는 열들 중에서의 최대높이에 의해 결정된다.
- 왼쪽에 있는 열들 중 최대높이는 '3'이고, 오른쪽에 있는 열들 중 최대 높이는 '4' 이다.
4. 3의 과정에서 구한 최대높이 중, 더 낮은 높이에 의해 결정된다.
- '3'과 '4'중에 더 낮은 높이인 '3'에 의해 결정된다.
5. 4의 과정에서 구한 높이와 현재 열의 높이의 차이 만큼 빗물이 고이게 된다.
- 4의 과정에서 구한 높이인 '3'과 현재 열의 높이인 '0'의 차이인 3 - 0 = 3 만큼의 빗물이 고이게 된다.
3번 열도 진행해보자. 3번 열의 높이 = 1
2. 나머지 열들을 해당 열을 기준으로 왼쪽에 있는 열, 오른쪽에 있는 열로 나눌 수 있다.
- 왼쪽에는 1열 2열이 존재하고, 오른쪽에는 4열 1개가 존재한다.
3. 왼쪽에 있는 열들 중에서의 최대높이와 오른쪽에 있는 열들 중에서의 최대높이에 의해 결정된다.
- 왼쪽에 있는 열들 중 최대높이는 '3'이고, 오른쪽에 있는 열들 중 최대 높이는 '4' 이다.
4. 3의 과정에서 구한 최대높이 중, 더 낮은 높이에 의해 결정된다.
- '3'과 '4'중에 더 낮은 높이인 '3'에 의해 결정된다.
5. 4의 과정에서 구한 높이와 현재 열의 높이의 차이 만큼 빗물이 고이게 된다.
- 4의 과정에서 구한 높이인 '3'과 현재 열의 높이인 '0'의 차이인 3 - 1 = 2 만큼의 빗물이 고이게 된다.
따라서 위의 경우, 빗물이 고일 수 있는 총량은 3 + 2 = 5가 된다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <iostream>
#define endl "\n"
#define MAX 510
using namespace std;
int H, W, Answer;
int Height[MAX];
int Max(int A, int B) { return A > B ? A : B; }
int Min(int A, int B) { return A < B ? A : B; }
void Input()
{
cin >> H >> W;
for (int i = 1; i <= W; i++) cin >> Height[i];
}
void Solution()
{
for (int i = 2; i < W; i++)
{
int Left, Right;
Left = Right = 0;
for (int j = 1; j < i; j++) Left = Max(Left, Height[j]);
for (int j = i + 1; j <= W; j++) Right = Max(Right, Height[j]);
int Result = Min(Left, Right) - Height[i];
if (Result >= 0) Answer += Result;
}
cout << Answer << endl;
}
void Solve()
{
Input();
Solution();
}
int main(void)
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
//freopen("Input.txt", "r", stdin);
Solve();
return 0;
}
|
cs |
'[ BOJ Code ] > # BOJ -' 카테고리의 다른 글
| [ 백준 2775 ] 부녀회장이 될테야 (C++) (0) | 2021.04.12 |
|---|---|
| [ 백준 2491 ] 수열 (C++) (0) | 2021.04.09 |
| [ 백준 2618 ] 경찰차 (C++) (4) | 2021.04.07 |
| [ 백준 3078 ] 좋은 친구 (C++) (4) | 2021.03.25 |
| [ 백준 11003 ] 최솟값 찾기 (C++) (1) | 2021.03.12 |