프로그래머스의 방문길이(Lv2) 문제이다.
[ 문제풀이 ]
주어진 명령어대로 움직였을 때, 캐릭터가 처음 걸어본 길의 길이를 구해야 하는 문제이다.
주어진 상황을 맵으로 어떻게 표현할지부터 정답을 도출하는 과정까지 순차적으로 알아보자.
#1. 맵 설정
먼저 주어진 맵을 한번 살펴보자.
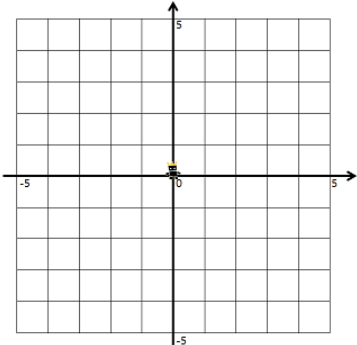
문제에서 제시한 맵의 형태이다. 가장 가운데 좌표가 (0 , 0)이고 해당 좌표를 기준으로 상하좌우에 따라서 좌표가 바뀌게 된다. 수학적 그림에 익숙한 우리 입장에서는 굉장히 익숙한 그림일 수 있지만, 프로그래밍으로 구현을 할 때에는 위와 같이 가장 가운데 좌표를 (0 , 0)으로 설정하면서 진행을 하기에는 불편한 점이 없지 않아 존재하게 된다.
그래서 본인은 단순하게 맵을 10 x 10짜리로 설정을 하고 시작점을 (5 , 5)로 주었다.
그리고 밑에서 구체적으로 이야기 하겠지만 이를 2차원 배열을 통해서 만들어 주었다.
#2. 처음 걸어본 길
맵을 설정했다면 이제는 캐릭터를 명령어에 맞게 움직여 주기만 하면 된다. 그렇다면 ! 우리가 구하고자 하는 처음 걸어본 길은 어떻게 구할 수 있을까 ??
가장 간단하게 접근했을 때, "이미 한번 움직인 좌표를 다시 방문하는 경우" 로 생각을 할 수 있다.
하지만, 좌표의 방문만으로는 걸었던 길을 또 걸었는지 아닌지에 대해서 판단하기가 어렵다.
다음과 같은 경우를 생각해보자.
현재 (5 , 5)에서 L - U - R - D 로 움직이는 경우를 생각해보자.
L - U - R - D 를 움직이게 되면, (5 , 5)를 우측 하단에 존재하는 꼭지점으로 만드는 정사각형이 하나 그려질 것이다. 가장 마지막 'D'에서는 다시 (5 , 5)로 오게 될 것이다.
그럼 시작할 때 (5 , 5)를 방문했고 마지막 'D'에 의해서 (5 , 5)를 재방문했으므로 마지막 'D'는 한번 움직인 좌표를 다시 방문한 경우이므로 걸었던 길을 또 걸은 것일까 ?? 그렇지 않다. 좌표를 재방문 했음에도 위의 예시에서 캐릭터가 처음으로 걸은 길의 길이는 4가 된다.
즉 ! 좌표의 재방문만으로는 구할 수가 없다. 그럼 어떻게 판단할 수 있을까 ??
여러가지 방법이 있겠지만 본인은 "좌표 + 방향" 으로 이를 판단해 주었다.
위의 예시를 "좌표 + 방향"의 개념으로 설명해보면 다음과 같다.
1. 'L'에 의해서 (5 , 5)에서 Left 방향으로 걸었습니다. 이 명령어에 의해 캐릭터가 (5 , 4)로 이동.
2. 'U'에 의해서 (5 , 4)에서 Up 방향으로 걸었습니다. 이 명령어에 의해 캐릭터가 (4 , 4)로 이동.
3. 'R'에 의해서 (4 , 4)에서 Right 방향으로 걸었습니다. 이 명령어에 의해 캐릭터가 (4 , 5)로 이동.
4. 'D'에 의해서 (4 , 5)에서 Down 방향으로 걸었습니다. 이 명령어에 의해 캐릭터가 (5 , 5)로 이동.
이 경우에는 같은 (5 , 5)를 2번 방문함에도 불구하고, 첫 번째 경우는 (5 , 5)에서 왼쪽으로 걸어가는 경우이고, 두 번째 경우는 (4 , 5)에서 아래쪽으로 내려오는 경우이므로 경로상으로는 겹치지가 않는다.
따라서 본인은 이를 좌표 + 방향을 이용해서 구현해 주었다.
실제 코드에서는 3차원 배열을 통해서 구현해 주었다.
bool Visit[10][10][4] 라는 3차원 배열을 통해서 판단해주었는데 이 배열의 의미는 다음과 같다.
Visit[x좌표][y좌표][방향(L/R/U/D)] = true : (x , y)에서 '방향' 으로 움직이는 경로는 이미 걸은적이 있습니다.
#3. 처음 걸어본 길 - 2
#2에서 좌표와 방향을 통해서 이미 걸었던 적이 있는 길인지 아닌지를 판단할 수 있다고 하였다.
그럼 다음과 같은 예시를 한번 보자.
(5 , 5)에서 시작해서 U - R - U - L - D - D 를 한번 살펴보자. 그림으로 그려보면 다음과 같다.
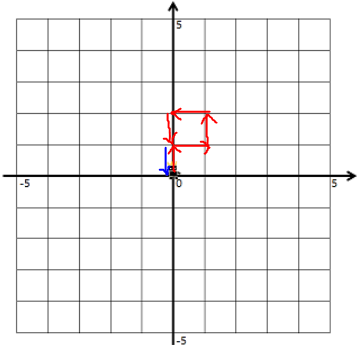
위와 같이 움직이게 되는데 가장 마지막 'D'를 의미하는 파랑색 화살표를 한번 살펴보자.
(5 , 5)를 기준으로 걸어간 길을 적어보면 가장 첫 명령어인 'U'에 의해서 (5 , 5)에서 Up으로 가는 길을 걸은 적이 있습니다 라고 표시가 될 것이다.
그런데 마지막 파랑색 화살표를 보게 되면 (4 , 5)에서 (5 , 5)로 내려오게 된다.그리고 이 명령어에 의해서 우리는
"(4 , 5)에서 Down으로 가는 길을 걸은 적이 있습니다" 라고 표시를 하게 될 것이다.
그리고 절대로 이게 이미 걸었던 길이라고 판단을 하지 못할 것이다. 왜냐하면 실제로 (4 , 5)에서 Down 방향으로 움직인 적이 없기 때문이다. 하지만 ! 위의 파랑색으로 표시된 길은 이미 걸었던 길이다. (5 , 5)에서 Up 방향으로 움직일 때 이미 걸은 길이 되는 것이다.
즉 ! 우리가 걸었던 길을 판단할 때, 단순히 현재 좌표(x , y)에서 'Dir'의 방향으로 움직인 적이 있었는지만 판단한다면 위와 같은 상황이 발생하게 된다. 이를 해결하기 위해서 움직인 후의 좌표인 (nx , ny)에서 역으로 움직인 적이 있었는지도 판단해 주어야 한다.
다시 위의 상황을 살펴보자.
(4 , 5)에서 (5 , 5)로 내려올 때, 단순히 "(4 , 5)에서 Down방향으로 움직인 적이 있나요?" 라고만 묻는것이 아니라,
"(4 , 5)에서 Down방향으로 움직인 적이 있나요?" + "(5 , 5)에서 Down의 역방향인 Up방향으로 움직인 적이 있나요?" 도 판단을 해줘야 한다는 것이다.
그래야만 우리가 구하고자 하는 정답을 구할 수 있다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
#include <string>
using namespace std;
int dx[] = { 0, 0, 1, -1 };
int dy[] = { 1, -1, 0, 0 };
bool Visit[15][15][4];
int Reverse(int Dir)
{
if (Dir == 0) return 1;
else if (Dir == 1) return 0;
else if (Dir == 2) return 3;
else if (Dir == 3) return 2;
}
int solution(string dirs)
{
int answer = 0;
int x = 5;
int y = 5;
for (int i = 0; i < dirs.length(); i++)
{
char C = dirs[i];
int nx;
int ny;
int Dir;
if (C == 'U')
{
Dir = 3;
nx = x + dx[3];
ny = y + dy[3];
}
else if (C == 'D')
{
Dir = 2;
nx = x + dx[2];
ny = y + dy[2];
}
else if (C == 'R')
{
Dir = 0;
nx = x + dx[0];
ny = y + dy[0];
}
else
{
Dir = 1;
nx = x + dx[1];
ny = y + dy[1];
}
if (nx < 0 || ny < 0 || nx > 10 || ny > 10) continue;
if (Visit[x][y][Dir] == false && Visit[nx][ny][Reverse(Dir)] == false)
{
answer++;
Visit[x][y][Dir] = true;
}
x = nx;
y = ny;
}
return answer;
}
|
cs |
'[ Programmers Code ] > # PG - Level2' 카테고리의 다른 글
| [ 프로그래머스 [ 3차 ] 압축 (Lv2) ] (C++) (0) | 2021.06.30 |
|---|---|
| [ 프로그래머스 배달 (Lv2) ] (C++) (11) | 2021.03.19 |
| [ 프로그래머스 n진수 게임 (Lv2) ] (C++) (0) | 2021.02.09 |
| [ 프로그래머스 순위 검색 (Lv2) ] (C++) (2) | 2021.02.01 |
| [ 프로그래머스 메뉴 리뉴얼 (Lv2) ] (C++) (0) | 2021.01.29 |