[ 백준 17611 ] 직각다각형 (C++)
백준의 직각다각형(17611) 문제이다.
[ 문제 바로가기 ]
[ 문제풀이 ]
직각 다각형의 수직선분과 수평선분에 가장 많이 교차하는 지점의 그 횟수를 구해야 하는 문제이다.
주어진 맵을 설정하는 과정부터 정답 도출하는 과정까지 순차적으로 진행해보자.
#1. 좌표 값 설정
먼저, 본격적인 문제를 풀기에 앞서 좌표값을 설정하는 과정부터 알아보자.
주어진 좌표값의 범위를 보게 되면 -500,000 ~ 500,000 사이라고 되어 있다. 이를 2차원 배열로 표현하게 되면 음수 값에 대한 좌표값을 설정해야 되는 경우가 발생하게 된다.
따라서, 본인은 모든 좌표값들에다가 +500,000 을 해 주었다. 예를 들어서 (-500000, -500000) 이 주어지더라도 +500,000을 해주게 되면 (0 , 0)이 되기 때문에 주어진 배열의 인덱스 값으로 표현이 가능하기 때문이다.
#2. 접근 방법
이제 본격적으로 문제를 풀어보자. 직각 다각형이라는 굉장히 이상한 모양의 도형들이 주어질텐데 여기서 임의의 위치에 선분을 그었을 때 가장 많은 교차지점을 찾아야 한다....
먼저, 입력으로 주어지는 선분들은 인접한 좌표값들 끼리는 서로 연결되어 있는 선분을 의미하게 된다.
예제입력1) 에서 보게 되면, 가장 처음에 (-1 , -1) 가 주어지고 그 이후에 (-1 , 1) 이 주어지게 되는데 이를 그림으로 표현해보면 다음과 같이 표현할 수 있다.

이와 같이 "세로선분" 으로 연결되어 있다는 것을 의미한다. 여기서 두 번째와 세 번째 입력 좌표를 살펴보면 (-1 , 1)과 (1 , 1)이 되는데 이를 위의 그림에서 이어서 표현해보면 다음과 같다.

위와 같은식으로 선분이 연결되어진다. 그럼 이를 통해서 뭘 알고싶어서 이런 당연한 이야기를 했는지 이야기해보자.
(x , y) 라는 선분과 (xx , yy) 라는 선분이 입력으로 주어진다면 다음과 같은 특징이 있다.
1. x == xx 인 경우, "세로 선분"이 만들어진다. ex) (-1 , -1) 과 (-1 , 1)을 이으면 세로선분이 만들어진다.
2. x != xx 인 경우, "가로 선분"이 만들어진다. ex) (-1 , 1)과 (1 , 1)을 이으면 가로선분이 만들어진다.
그렇다면, 위의 세로선분과 가로선분이 만들어진다는 것이 무엇을 의미하는 것일까 ???
극단적인 이야기를 한번 해보자. 세로선분이 하나 있을 때, 교차 지점을 구하기 위해서는 무슨 선분을 만들어 주어야 할까 ??

위와 같이, 세로선분과의 교차되는 횟수를 구하기 위해서는 빨강색으로 표시된 가로선분을 놓아봄으로써 교차 지점을 구할 수가 있다.
반대로, 가로선분이 만들어진다는 것은 교차 지점을 구하기 위해서는 세로 선분을 만들어 주어야 한다는 것을 의미한다.

위와 같이 가로선분이 만들어 진다면, 우리는 가로선분에다가 세로 선분을 그어봄으로써 교차횟수를 계산을 할 수가 있다.
우리는, 이를 이용해서 문제를 해결해 나갈 것이다.
#3. 교차지점 및 횟수 구하기
그럼 지금부터 교차가 시작되는 첫 지점과 마지막 지점에 대해서만 계산을 한번 해볼 것이다.
무슨 말인지 이해를 하기 위해서 먼저 그냥 결론부터 이야기를 해보자. 우리는 다음과 같이 교차지점을 구할 것이다.

이와 같은 직각다각형이 있다고 가정해보자. 그리고 먼저, 아래 그림과 같이 빨강색 가로선분이 아래에서 위쪽으로 한칸 씩 올라가는 상황이라고 시뮬레이션을 한번 해보자.

그럼 올라가면서 뭐 이런 상황들이 발생하게 될 것이다.

그리고 각각의 선분들이 가지는 교차지점의 횟수 중에 최댓값을 구하면 될 것이다. 그런데 ! 저기서 발생하는 교차지점의 횟수를 구하기 위해서 1차적으로 "만들어 지는 선분의 시작 지점과 마지막 지점의 교차 횟수만 Count" 하는 과정을 진행할 것이다.

가장 먼저, 파랑색 선분이 그어졌다고 가정해보자. 파랑색 선분은 세로 선분이기 떄문에 #2에서 했던 이야기에 의하면, 세로선분이 만들어 진 것은, (1)번 좌표와 (2)번 좌표의 'x'좌표가 동일하다는 것을 의미한다. (좌표를 편의상 (x, y) 라고 표현하겠다.)
그럼 (1)번 좌표를 (x , y) , (2)번 좌표를 (x , yy) 라고 설정해보자.
그리고, 선분은 세로선분이기 때문에 가로 선분을 그었을 때의 교착 지점을 구하는 것만이 의미가 있다.
그럼, 저 위에서 했던 그림과 같이 임의의 빨강색 선이 아래에서 부터 한칸씩 순차적으로 올라온다고 가정해보자. 그럼 (1)번 지점이 되는 순간 교차되는 횟수가 하나 더 더해질 것이다. 그림으로 표현해보면 다음과 같다.
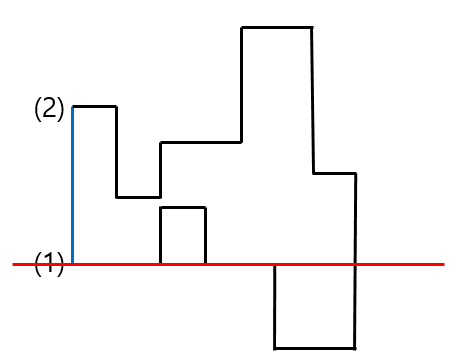
이렇게 되는 순간, (1)번 지점에 있는 'y'좌표와 교차됨으로써 교차 횟수가 하나 더 증가하게 될 것이다.
"어 직각다각형의 오른쪽 부분을 보면, 교차 횟수가 하나만 더 증가하는 것이 아니라 여러 군데 더 증가하는 것 처럼 보이는데?" 라고 생각할 수 있지만, 저 부분도 다 나중에 계산을 할 것이다. 지금 오른쪽 부분을 모른채, 가장 첫 번째 선분인 파랑색 선분에 대해서만 계산을 하고 있는 것이다.
그러다가, 빨강선이 계속 쭉 올라가서 (2)번 지점까지 갔다고 가정해보자. (2)번 지점 이후로부터는 교차지점이 하나가 줄어들게 된다. 왜 ?? (1)번과 (2)번이 만들고 있는 파랑색 선분이 끝나버리기 때문이다.

그림으로 표현해보면, 빨강색 선분이 (2)번 지점보다 더 올라가게 되는 순간 교차되는 횟수가 하나 줄어들게 된다.
그래서, (1)번 지점에서는 교차되는 횟수가 하나 증가한다는 것과, (2)번 지점에서는 교차되는 횟수가 하나 감소한다는 것을 표현해 줄 것이다. 이러한 과정을 모든 선분들에 대해서 다 해줄 것이다. 물론, "가로선분"과 "세로선분"을 구별하면서 진행을 해줄 것이다.
코드로 나타내면 다음과 같다.
int x = Coord[i].first;
int y = Coord[i].second;
int nx = Coord[(i + 1) % N].first;
int ny = Coord[(i + 1) % N].second;
if(x == nx)
{
int Max_Y = max(y, ny);
int Min_Y = min(y, ny);
Count_Y[Min_Y]++;
Count_Y[Max_Y]--;
}
else
{
int Max_X = max(x, nx);
int Min_X = min(x, nx);
Count_X[Min_X]++;
Count_X[Max_X]--;
}위의 코드에서 'Coord'라고 나와있는 Vector는 입력 좌표들을 넣어놓은 Vector이다.
그리고, Count_Y[] 라는 배열과 Count_X[] 라는 배열이 있는데 이 배열들이 가지는 값은 다음과 같다.
Count_X[A] : 세로선분을 그었을 때, x좌표가 A인 지점에서 교차되는 횟수
Count_Y[A] : 가로선분을 그었을 때, y좌표가 A인 지점에서 교차되는 횟수
우리가 위에서 (1)번과 (2)번 지점을 이은 파랑색 선으로 이야기를 했었는데, 파랑색 선분은 세로 선분이기 떄문에 if(x == nx) 라는 조건문에 들어가게 될 것이다.
그리고 (1)번 지점에서는 교차되는 횟수가 증가했으므로, Count_Y[]의 값이 ++ 되고 있고, (2)번 지점에서는 Count_Y[]의 값이 -- 되는 것을 확인할 수 있다.
그런데 ! 우리는 여기까지만 보면, "입력으로 주어지는 좌표들에 대한 Count값만 계산" 했다는 것을 알 수 있다.

이와 같이 선분의 가운데에 있는 지점들에 대해서는 계산이 안 되어 있다는 것이다. 이 값들 중에서 정답이 있을 수도 있기 때문에 이 값 또한 모두 구해주어야 한다. 이를 어떻게 구할 수 있을까 ??
누적합의 개념으로 다음과 같이 구할 수가 있다.
for(int i = 1; i < MAX; i++)
{
Count_X[i] += Count_X[i - 1];
Count_Y[i] += Count_Y[i - 1];
}기존의 교차횟수만큼 계속해서 더해지게 될 것이다. 그러다보면, 어떤 경우에는 선분이 끝나서 음수값을 가지고 있어서 교차횟수가 감소할 것이고 어떤 경우에는 계속해서 더해지게 될 것이다.
이를 통해서 모든 좌표에 대해서 값을 구한 후에 최댓값을 찾을 수 있다.
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
// x좌표가 같다 = 수직선
// y좌표가 같다 = 수평선
#include <iostream>
#include <vector>
#include <algorithm>
#define ALPHA 500000
#define MAX 1000010
using namespace std;
int N;
int Count_X[MAX];
int Count_Y[MAX];
vector<pair<int, int>> Coord;
void Input()
{
cin >> N;
for(int i = 0 ; i < N; i++)
{
int a, b; cin >> a >> b;
a += ALPHA;
b += ALPHA;
Coord.push_back(make_pair(a, b));
}
}
void Solution()
{
for(int i = 0 ; i < N; i++)
{
int x = Coord[i].first;
int y = Coord[i].second;
int nx = Coord[(i + 1) % N].first;
int ny = Coord[(i + 1) % N].second;
if(x == nx)
{
int Max_Y = max(y, ny);
int Min_Y = min(y, ny);
Count_Y[Min_Y]++;
Count_Y[Max_Y]--;
}
else
{
int Max_X = max(x, nx);
int Min_X = min(x, nx);
Count_X[Min_X]++;
Count_X[Max_X]--;
}
}
for(int i = 1; i < MAX; i++)
{
Count_X[i] += Count_X[i - 1];
Count_Y[i] += Count_Y[i - 1];
}
int answer = 0;
for(int i = 1; i < MAX; i++)
{
answer = max(max(Count_X[i], Count_Y[i]), answer);
}
cout << answer << endl;
}
void Solve()
{
Input();
Solution();
}
int main(void)
{
Solve();
return 0;
}
|
cs |