[ 프로그래머스 N개의 최소공배수 (Lv2) ] (C++)

프로그래머스의 N개의 최소공배수(Lv2) 문제이다.

 

[ 문제풀이 ]

문제를 해결하기 위해서 사용되는 정말 간단한 수학 공식에 대해서 이야기를 하고 이를 통해 정답을 도출하는 과정까지 진행해보자.

N개의 최소공배수를 구해야 하는 문제이니 최소 공배수를 구하는 과정부터 알아보자.

 

#1. 두 수의 최소 공배수

정말 간단한 예시를 한번 가지고 진행해보자.

숫자 '12'와 '18' 이 있다. 이 2개의 숫자의 최소공배수는 두 수의 공약수로 나눠가는 방식으로 쉽게 구할 수 있다.

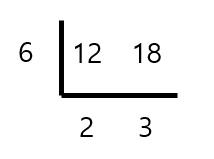
12와 18은 '6'이라는 공약수로 나눌 수가 있다. 그 때의 몫은, '2'와 '3'이 된다.

그리고 '2'와 '3'의 공약수는 1을 제외하고는 없기 때문에, 즉, 서로소의 관계를 가진 숫자들이기 때문에  더 이상 나눠지지가 않는다.

따라서, 이 때의 최소공배수는 6 x 2 x 3 = 36 이 된다.

물론, 소인수분해를 통해서도 쉽게 구할 수 있다.

12 = 2^2 * 3

18 = 2 * 3^2 이기 때문에 최소공배수는 2^2 * 3^2이 되어서 4 * 9 = 36 이 된다.

그런데 여기서, 숫자 '6'은 12와 18의 최대공약수이다. 그럼 이제 이를 문자로 바꿔서 표현해보자.

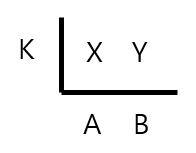
X와 Y라는 숫자가 있다. 이 숫자들의 최소공배수는 K * A * B 라는 것을 알 수 있다.

또한, X = A * K 로 표현할 수 있고, Y = B * K  로 표현할 수 있다.

그럼 여기서 X * Y 를 다르게 한번 표현해보자. 여기서 갑자기 이걸 왜 표현하는지는 이해가 잘 안될 수 있지만, 왜 했는지에 대해서는 밑에서 이야기하도록 하고 X * Y를 한번 표현해보자.

X * Y 는 이렇게 표현할 수 있다.

X * Y = (K * A) * (K * B) = K * K * A * B

그런데 ! 여기서 X * Y = K * K * A * B 에서 빨강색으로 표시한 부분을 보자.

빨강색으로 표시한 부분은 무슨 값일까 ?? 위에서도 이야기했듯이, K * A * B는 X와 Y의 "최소공배수"가 된다.

즉, [ X * Y = K * 최소공배수 ] 라는 수식이 성립하게 된다.

최소공배수를 구하기 위해서 K를 양변에 나눠버리게 되면 [ 최소공배수 = (X * Y) / K ] 가 된다.

그리고, 여기서 K는 X와 Y의 "최대공약수" 이다.

즉 ! "최소공배수 = 두 수의 곱 / 최대공약수" 로 구할 수가 있다.

 

#2. 두 수의 최대 공약수

우리는 #1의 과정에서, 최소공배수를 구하기 위해서는 두 수의 최대공약수만 구한다면, 쉽게 구할 수 있다는 것을 이야기 했다.

그럼, 두 수의 최대 공약수를 한번 구해보자.

최대 공약수를 구하는 알고리즘으로는 "유클리드 호제법" 이라는 것이 있다.

간략하게 이야기해보면, 2개의 숫자가 서로 나누어 떨어지지 않을 시에는 더 큰 숫자를 작은 숫자로 나눴을 때의 나머지를 구하고... 더 작은 숫자와 나머지의 관계를 통해서 나머지를 구하고... 뭐 이런 식이다..

사실.. 본인도 유클리드 호제법이 어떻게 실행되고 동작하는지는 알고 있지만 정확하게 어떤 원리에 의해서 이런 알고리즘이 성립하는지는 잘 모르겠다.. 잘 모르는 채로 이런 문제가 나왔을 때 유용하게 사용하고 있다....

하나의 예시로 유클리드 호제법이 돌아가는 방식에 대해서 이야기를 해보자.

'12'와 '18'의 최대공약수를 구해보자.

12와 18 중에서 더 큰수는 '18', 더 작은 수는 '12'가 된다.

이 2개의 숫자는 서로 나누어 떨어지지 않는다. 이 경우에는 큰 숫자를 작은 숫자로 나눴을 때의 나머지를 구해준다.

18을 12로 나누게 되면 나머지가 '6'이 나오게 된다.

그럼 이제, 작은 숫자와 나머지 2개의 숫자를 비교하게 된다.

즉 ! 12와 6을 비교해보는 것이다. 이 2개의 숫자는 서로 나누어 떨어지는 숫자이다. 이 때는 더 이상 나머지를 구할 필요 없이 더 작은 숫자인 '6'이 최대공약수로 선택이 된다.

뭐 이런식으로 진행되는게 유클리드 호제법이다.. 구체적인 내용은 위키백과를 참고하도록 하자..

 

위와 같이 최대 공약수를 구하는 과정을 코드로 나타내면 다음과 같다.

int Gcd(int a , int b)
{
    int A = max(a, b);
    int B = min(a, b);
    
    while(A % B != 0)
    {
        int R = A % B;
        A = B;
        B = R;
    }
    return B;
}

정말 말 그대로, 2개의 숫자 중 큰 숫자와 작은 숫자로 나누어서 2개의 숫자가 나누어 떨어질 때 까지 나머지를 구하는 과정을 반복해주는 과정이다. 위와 같은 방법으로 우리는 "최대공약수"를 구할 수 있다.

 

#3. N개의 최소공배수

#1에서는 숫자 2개의 최소공배수를 구하는 과정을 이야기했다.

그 결과, 최소공배수 = 두 수의 곱 / 최대 공약수 라는 것을 알 수 있었고, #2에서는 최대 공약수를 구하는 방법까지 알아냈다.

그런데 우리는 결국 2개의 최소공배수가 아닌, N개의 숫자의 최소공배수를 구해야 한다.

이는 어떻게 구할 수 있을까 ??

[ A , B , C , D ] 가 있을 때 이 A, B, C, D의 최소공배수는 얼마가 될까 ???

2개씩 묶어서 구할 수가 있다.

A와 B의 최소공배수 = x

x와 C의 최소공배수 = y

y와 D의 최소공배수 = z

A, B, C, D의 최소공배수는 'z'가 된다는 것이다. 한번 확인해보자

[ 2 , 3 , 4, 5 ] 가 있다. 2, 3, 4, 5의 최소공배수는 ??

2와 3의 최소공배수 = 6

6과 4의 최소공배수 = 12

12와 5의 최소공배수 = 60

2, 3, 4, 5의 최소공배수 = 60

순서에 상관이 없다.

3과 5의 최소공배수 = 15

2와 4의 최소공배수 = 4

15와 4의 최소공배수 = 60

2, 3, 4, 5의 최소공배수 = 60

 

즉 ! 우리는 #1과 #2에서 구한 최소공배수를 N개의 숫자들에 대해서 모두 반복해주면 결과적으로 N개의 최소공배수를 구할 수 있다.

 

[ 소스코드 ]

#include <string>
#include <vector>
#include <algorithm>
using namespace std;
 
int Gcd(int a , int b)
{
    int A = max(a, b);
    int B = min(a, b);
    
    while(A % B != 0)
    {
        int R = A % B;
        A = B;
        B = R;
    }
    return B;
}
 
// 최소공배수 = 두 수의 곱 / 최대공약수
int solution(vector<int> arr) 
{
    int answer = arr[0];
    for(int i = 1; i < arr.size(); i++)
    {
        int GCD = Gcd(answer, arr[i]);
        int LCM = answer * arr[i] / GCD;
        answer = LCM;
    }
    return answer;
}