[ 백준 21611 ] 마법사 상어와 블리자드 (C++)
백준의 마법사 상어와 블리자드(21611) 문제이다.
[ 문제 바로가기 ]
[ 문제풀이 ]
마법사 상어가 블리자드 마법을 M번 시전했을 때, 그 과정에서 폭발한 구슬의 갯수를 구해야 하는 문제이다.
주어진 맵을 관리하는 과정부터 정답을 도출하는 과정까지 진행해보자.
#1. 맵 관리
문제를 보면, 시작하자마자 조금 골치아픈 부분이 하나 등장한다. 바로 맵이 정상적인 모습을 하고 있는 것이 아니라는 것이다. 그럼 지금부터 맵을 세팅하는 과정부터 알아보자.
기본적으로 맵은 가장 한 가운데 좌표(N / 2 , N / 2)에서부터 뱅글뱅글(?) 돌아가는 형태로 존재하게 된다.

빨강색으로 동그라미 친 좌표는 (N / 2 , N / 2)가 될 것이다. 그리고 지금부터 회전을 시작할 것인데 회전은 다음과 같이 진행된다.

위와 같이 회전을 하게 된다. 이제부터는 위의 그림을 "화살표의 색깔" 별로 한번 살펴보자.
가장 처음, 한 가운데 좌표에서 시작을 하게 되면 다음과 같이 진행이 되어진다.
1. 검은색 화살표 처럼 서쪽으로 '1칸' 이동하게 된다. [ 진행방향 = 서쪽 ]
2. 검은색 화살표 처럼 남쪽으로 '1칸' 이동하게 된다. [ 진행방향 = 남쪽 ]
3. 파랑색 화살표 처럼 동쪽으로 '2칸' 이동하게 된다. [ 진행방향 = 동쪽 ]
4. 파랑색 화살표 처럼 북쪽으로 '2칸' 이동하게 된다. [ 진행방향 = 북쪽 ]
5. 빨강색 화살표 처럼 서쪽으로 '3칸' 이동하게 된다. [ 진행방향 = 서쪽 ]
6. 빨강색 화살표 처럼 남쪽으로 '3칸' 이동하게 된다. [ 진행방향 = 남쪽 ]
7. 주황색 화살표 처럼 동쪽으로 '4칸' 이동하게 된다. [ 진행방향 = 동쪽 ]
8. 주황색 화살표 처럼 북쪽으로 '4칸' 이동하게 된다. [ 진행방향 = 북쪽 ]
9. 초록색 화살표 처럼 서쪽으로 '5칸' 이동하게 된다. [ 진행방향 = 서쪽 ]
위와 같이 진행하게 되는데, 우리는 이 과정에서 특별한 규칙을 몇 가지 찾을 수 있다.
먼저, "진행방향" 을 살펴보자.
진행방향은, 서 - 남 - 동 - 북 순서로 계속해서 바뀌면서 진행된다는 것을 알 수 있다.
그리고, 이동하는 칸 수를 확인해보자.
1 ~ 2번 과정에 의해서 '1칸' 이동하는 과정을 '2번' 진행하였다.
3 ~ 4번 과정에 의해서 '2칸' 이동하는 과정을 '2번' 진행하였다.
5 ~ 6번 과정에 의해서 '3칸' 이동하는 과정을 '2번' 진행하였다.
7 ~ 8번 과정에 의해서 '4칸' 이동하는 과정을 '2번' 진행하였다.
9번 과정에 의해서 '5'칸 이동하는 과정을 최종적으로 진행하였다.
딱 보면 알 수 있듯이, "움직여야 하는 칸 수"는 1칸부터 시작해서 계속해서 증가하게 되고, 그리고 각각의 움직여야 하는 칸수는 모두 2번씩 실행된다는 것을 알 수 있다.
우리는 위와 같은 특징 및 규칙들을 이용해서 "주어진 맵에서, 각 좌표가 가지는 번호" 에 대해서 파악할 수 있다.
여기서 '번호' 라는 것은 입력으로 주어지는 구슬의 번호를 의미하는 것이 아니다. 다음과 같은 번호이다.

위의 그림이 5 x 5 맵에서 각 좌표들이 가지는 번호들이다. 이 번호들을 위의 규칙들을 이용해서 파악할 수 있는 것이다.
그렇다면 ! 지금 위의 과정을 왜 했을까 ?? 무엇을 하기 위해 진행하였을까 ??
사실 본인은 위의 과정을 진행한 이유가 "전체적인 구현을 편하게 하기 위해서" 이다.
우리는 지금부터 문제를 해결할 때 까지 계속해서 위와 같이 뱅글뱅글 도는 형태로 맵을 바라봐야 한다.
그럼, 그럴 때 마다 위에서 이야기한 규칙들 대로 구현을 해주면서 진행을 해줘야 한다. 물론 이렇게 하더라도 큰 문제가 되지는 않을 것인데 너무 불편할 것 같아서 본인은 "맵의 번호를 통해서 좌표에 직접적으로 접근이 가능" 하도록 만들어 주었다.
예를 들어서 맵의 1번자리 ! 라고 한다면 바로 (2 , 1) 이 나오도록 , 혹은 맵의 10번자리 ! 라고 한다면 바로 (2 , 0)이 나올 수 있도록 만들어 준 것이다. 반대로도 가능하도록 만들어 주었다. 예를 들어서 (2 , 1) ! 이라고 하면 바로 1번자리라는 정보가 나올 수 있도록, 혹은 (2 , 0) ! 이라고 한다면 바로 10번 자리 라는 정보가 나올 수 있도록 만들어 준 것이다.
먼저, 코드로 살펴보고 이야기를 더 해보자.
struct COORD
{
int x;
int y;
};
int N_MAP[MAX][MAX];
COORD Shark;
COORD Coord[MAX * MAX];
void Make_MAP()
{
int x = N / 2;
int y = N / 2;
int Move_Cnt = 1;
int Num = 0;
int Dir = 3;
Shark = { x , y };
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
while (1)
{
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < Move_Cnt; j++)
{
x += dx[Dir];
y += dy[Dir];
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
}
Dir = Change_Dir(Dir);
}
Move_Cnt++;
if (Move_Cnt == N)
{
for (int j = 0; j < Move_Cnt; j++)
{
x += dx[Dir];
y += dy[Dir];
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
}
break;
}
}
}
가장 먼저, 좌표에 대한 정보를 저장하기 위한 구조체 COORD 를 선언해 주었다. 물론 구조체를 선언하지 않고 pair로 관리하더라도 상관은 없다.
그리고 선언되어 있는 변수들에 대해서 부터 이야기를 해보자.
1. N_MAP[][] : Number_MAP
- N_MAP[][] 2차원 배열은 "좌표를 통해서 해당 좌표의 번호를 가져오기 위해 선언된 변수" 이다.
- N_MAP[A][B] = C의 의미는 "(A , B)라는 좌표는 C라는 번호를 가지고 있습니다." 를 의미한다.
- ex) N_MAP[2][0] = 10 , N_MAP[2][1] = 1
2. Coord[]
- Coord[] COORD형 1차원 배열은 "번호를 통해서 해당 번호의 좌표를 가져오기 위해 선언된 변수" 이다.
- Coord[A] = { B , C } 의 의미는 "맵에서 A번은 (B , C)에 위치하고 있습니다" 를 의미한다.
- ex) Coord[1] = { 2 , 1 } , Coord[10] = { 2 , 0 }
그리고 위의 2가지 변수들을 채워나가기 위해서 우리가 지금까지 진행했던 규칙들이 필요하다.
Make_MAP() 함수 안에 구현된 내용을 확인해보면...
"움직이는 칸 수는 1칸 부터 시작해서 꾸준히 증가하는 형태를 가지고, 이 움직이는 칸 수가 2번씩 진행된다" 라는 것을 구현해 놓은 것이다.
이 변수들을 앞으로 어떻게 사용할 것인지는 차례차례 진행해보면서 이야기를 더 해보자.
#2. 얼음 파편 던지기
상어가 주어진 방향과 칸 수로 얼음파편을 던지게 되면, 해당 칸들은 구슬이 없어지게 된다.
그럼 문제에서 설명으로 나와있는 그림을 통해서 이 과정을 구체적으로 알아보자.

이 상태에서 상어가 아래 방향으로 2칸 얼음 파편을 던지게 되면 다음과 같은 부분이 얼음파편에 맞게 된다.

그럼 우리는 상어의 좌표를 기준으로 "움직인 방향 + 칸수" 만큼에 존재하는 모든 구슬들을 '0'으로 바꿔줘버리면 될 것이다. 왜냐하면 이 문제에서 '0'으로 입력되어 있는 부분은 "구슬이 존재하지 않는 빈칸" 이기 때문이다.
하지만 본인은 이 과정에서 '0'으로 바꿔주지 않았다. 대신, "얼음파편에 의해서 구슬이 파괴된 좌표입니다" 라고 표시는 해 주었다.
void Blizzard_Magic(int Idx)
{
memset(Delete, false, sizeof(Delete));
int Dir = Cmd[Idx].first;
int K = Cmd[Idx].second;
int x = Shark.x;
int y = Shark.y;
for (int i = 0; i < K; i++)
{
x += dx[Dir];
y += dy[Dir];
Delete[N_MAP[x][y]] = true;
}
}위의 과정을 코드로 나타낸 부분이다.
얼음파편의 공격을 받은 좌표들을 파악한 후에, 0으로 바꿔주는 과정이 아닌, Delete[] 라는 bool형 1차원 배열을 이용해서 "얼음 파편에 의해서 구슬이 파괴된 좌표입니다" 라고 표시만 해 주었다.
또한 ! 좌표에 표시를 해주는 것이 아닌, #1의 과정에서 선언해놓은 N_MAP 변수를 통해서 이 맵에서 몇 번 위치에 있는 구슬이 파괴되었는지를 표시해 주었다.
Delete[A] = true의 의미는 "이 맵에서 A번에 위치한 구슬은 파괴되었습니다" 를 의미한다.
그럼 왜 이렇게 0으로 바꿔주지 않는지는 다음 과정에서 구체적으로 알아보자.
#3. 구슬 움직이기
이제 구슬이 파괴되어 빈칸이 생겼으니 구슬을 움직여 줘보자. 그리고 이 과정은 밑에서 또 한번 사용되어야 하니, 블리자드 마법을 사용했을 때만 적용되는것이 아닌, 구슬 사이사이에 빈칸이 생겼을 때 구슬들을 움직일 수 있도록 일관적으로 구현을 해보자.

위의 그림에서 번호 순서대로 움직여야 하는 칸 수에 대해서 생각을 한번 해보자.

본인이 색깔을 한번 넣어보았다. 그리고 편의를 위해 오른쪽 맵은 맵에서의 번호를 나타낸 맵이다.
먼저, 파랑색으로 표시된 1, 2번 구슬들은 움직일 필요가 없을 것이다.
빨강색으로 표시된 3번 구슬같은 경우에는 블리자드 마법에 의해서 파괴된 구슬이니 넘어가자.
초록색으로 표시된 4번 ~ 13번 같은 경우에는 앞으로 한 칸씩 움직여 줘야 할 것이다.
왜냐하면 3번 구슬이 파괴되었기 때문에, 그 빈 칸을 채우기 위해서 한 칸씩 앞으로 움직여 줘야 할 것이다.
빨강색으로 표시된 14번 구슬같은 경우에는 블리자드 마법에 의해서 파괴된 구슬이니 넘어가자.
노랑색으로 표시된 15 ~ 39번 구슬 같은 경우에는 앞으로 "2칸"씩 움직여 줘야 할 것이다.
왜냐하면, 3번 구슬이 파괴됨으로써 1칸씩 앞으로 움직여 줘야 할 것이고, 14번 구슬이 파괴됨으로써 1칸씩 앞으로 움직여 줘야 하므로 총 2칸씩 움직여 줘야 할 것이다.
즉 ! "번호순서대로 탐색을 하면서, "자기 앞에서 몇 개의 구슬이 파괴되었는지"에 따라서 움직여야 하는 칸 수가 결정" 되어 지는 것이다.
다시 한번 이야기를 해보자.
1 ~ 2번 구슬 같은 경우에는, 자기 앞에서 구슬이 0개 파괴되었다. 즉, 파괴된 구슬이 없으므로 움직일 필요가 없다.
4 ~ 13번 구슬 같은 경우에는, 자기 앞에서 '3'번 구슬 1개가 파괴되었다. 즉, 파괴된 구슬의 갯수인 1만큼 앞으로 움직여 주어야 한다.
15 ~ 39번 구슬 같은 경우에는, 자기 앞에서 '3'번 구슬, '14'번 구슬 2개가 파괴되었다. 즉, 파괴된 구슬의 갯수인 2만큼 앞으로 움직여 주어야 한다.
그럼 ! 이를 어떻게 구현을 할 수 있을까 ?? 또 맵을 빙글빙글 돌면서 구현을 해야할까 ??
그렇지 않다. 이를 위해서 우리는 번호별로 어떤 좌표를 가지고 있는지 #1에서 Coord라는 변수에 모두 저장을 해 주었다.
즉 ! 구슬을 옮기기 위한 과정을 나타내면 다음과 같다.
1. 파괴된 구슬이라면, "현재까지 파괴된 구슬의 갯수"를 ++ 해주고 넘어가면 된다.
2. 파괴되지 않은 구슬이라면, "현재까지 파괴된 구슬의 갯수만큼 맵의 번호를 앞당겨서 저장"
해주면 된다.
2번 과정을 조금 더 구체적으로 이야기하면 다음과 같다.
위의 그림에서 '4번'구슬을 한번 살펴보자. 4번 구슬은 자기 앞에서 '1개'의 구슬이 파괴되었기 때문에, 4번 구슬은 4 - 1인 3번 구슬이 위치했던 자리에 가게 된다.
'15번' 구슬을 한번 살펴보자. 15번 구슬은 자기 앞에서 '2개'의 구슬이 파괴되었기 때문에, 15번 구슬은 15 - 2 = 13번 구슬이 위치했던 자리에 가게 된다.
우리가 #1에서 선언했던, 수식으로 이를 표현해보자.
Coord[A] = { x , y } : 맵에서 A번은 좌표로 (x , y)에 위치합니다. 라는 변수를 선언해 주었다.
int Cnt : 현재까지 파괴된 구슬의 갯수
int Num : 현재 구슬이 위치한 맵의 번호
라고 둔다면...
MAP[Coord[Num - Cnt].x][Coord[Num - Cnt].y] = MAP[Coord[Num].x][Coord[Num].y];위와 같은 식으로 표현을 할 수가 있다. 이를 위해서 ! #1에서 Coord를 선언해서, 번호가 가지는 좌표정보를 저장해놓은 것이다.
하지만 우리에게는 해결되지 않은 정보가 한 가지 더있다.
왜 #2의 과정에서, 블리자드 마법에 의해서 파괴된 구슬을 왜 바로 '0'으로 바꾸지 않고 따로 체크만 해주었을까 ??
바로 이를 구분하기 위해서이다.

만약 #2의 과정에서 파괴된 구슬을 바로 0으로 바꿨다고 가정해보자. 그럼 위의 그림과 같이 빨강색으로 표시된 "파괴된 구슬"과 주황색으로 표시된 "애초에 구슬이 존재하지 않았던 칸"을 구분할 수 있을까 ??
이를 구분할 수가 없다. 그럼 구분을 안하면 어떤 일이 발생하게 될까 ??
가장 마지막 부분이 이상하게 변질되는 현상이 발생할 수 있다. 무슨 상황인지 알아보기 전에 코드로 확인해보고 이야기를 해보자.
void Move_Marble()
{
bool Flag = false;
int Cnt = 0;
for (int i = 1; i < N * N; i++)
{
if (Delete[i] == true)
{
Flag = true;
Cnt++;
}
else
{
if (MAP[Coord[i].x][Coord[i].y] == 0)
{
for (int j = 1; j <= Cnt; j++) MAP[Coord[i - j].x][Coord[i - j].y] = 0;
Flag = false;
break;
}
else MAP[Coord[i - Cnt].x][Coord[i - Cnt].y] = MAP[Coord[i].x][Coord[i].y];
}
}
if (Flag == true)
{
int i = (N * N) - 1;
for (int j = 0; j < Cnt; j++, i--) MAP[Coord[i].x][Coord[i].y] = 0;
}
}본인이 구현한 구슬이 움직이는 과정이다.
맵의 1번부터 차례대로 탐색을 진행하는데, 중간에 "블리자드 마법에 의해서 파괴된 구슬"을 만나게 되면 "현재까지 파괴된 구슬의 갯수"가 ++ 하는 과정을 확인할 수 있다.
그리고, 만약 파괴되지 않은 구슬이라면 line20)에서 현재까지 파괴된 구슬의 갯수만큼 앞당기게 하는 과정을 확인할 수 있다. 그럼 line14 ~ 19)의 과정을 한번 살펴보자.
이 과정은 맵에서 '0'인 칸을 만났을 때이다. 즉 ! 원래부터 애초에 구슬이 있지 않은 칸을 만났을 때이다. 이 경우에는 더 이상의 탐색이 필요하지 않다. 다만 마지막부분을 '0'으로 바꿔주는 과정이 필요하다. 저 과정이 없다면 아래와 같은 상황이 발생하게 된다.

위의 그림에서 빨강색으로 표시된 2칸을 파괴한 후에, 구슬이 움직이게 된다면 다음과 같이 변하게 된다.

왼쪽 그림이 정상적으로 구슬이 움직인 상황이고, 오른쪽 그림은 잘못된 상황이다.
line14 ~ 19)가 오른쪽 그림을 왼쪽 그림으로 만들어주는 역할을 해준다.
즉 ! "애초에 구슬이 없었던 위치"를 만나게 된다면, "파괴된 구슬의 갯수" 만큼의 가장 마지막 숫자들을 0으로 바꿔주어야 한다. 위에서 보면 블리자드 마법에 의해서 2개의 구슬이 파괴되었고, 가장 마지막 숫자(노랑색으로 표시되있는 곳) '2개'를 0으로 바꿔주는 것이다.
그렇다면 위의 코드에서 line 24 ~ 28)은 무엇을 위한 부분일까 ??
위의 맵을 다음과 같이 한번 바꿔보자.

맵이 위와 같은 형태에서 빨강색 2칸이 블리자드에 의해서 파괴되었다고 가정해보자.
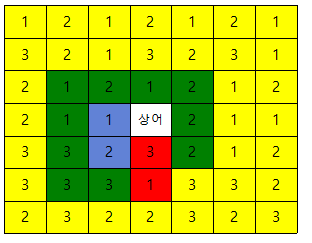
그럼 위와 같이 색깔별로 파랑색, 초록색, 노랑색이 0칸, 1칸, 2칸씩 앞당겨지게 될 것이다.
하지만 ! 위의 코드에서 line14 ~ 19)에는 절대 걸리지 않을 것이다. 왜냐하면 애초부터 구슬이 없었던 칸은 없기 때문이다. 즉 ! 이런 경우를 위해서 line24 ~ 28)이 존재하는 것이다.
그럼 다시 본론으로 돌아와보자. 우리가 어떤 이야기를 하고 있었을까 ?
굳이 블리자드 마법에 의해서 깨진 구슬들을 바로 '0'으로 바꾸지 않은 이유에 대해서 이야기를 하고 있었다.
이 이유가 바로 위의 상황 때문이다. 만약, 구슬을 바로 '0'으로 바꿔버리고, 파괴된 구슬의 갯수를 Count하기 위해서 '0'을 만날 때 마다 ++ 를 시켜버린다면, line14 ~ 19)에 의해서 파괴된 구슬의 갯수가 Count가 잘못될 것이고 line24 ~ 28)에 의해서 마지막 정리하는 부분에 구슬들이 잘못 표기되는 경우가 발생하기 때문이다.
이와 같은 이유 때문에 ! 블리자드 마법에 의해서 구슬이 파괴되더라도 체크만 해주고 바로 '0'으로 바꿔주지 않은 것이다.
#4. 연속된 구슬 파괴하기
4번째 과정이다. 4개 이상 연속된 구슬들을 모두 파괴해야 하는 것이다.
이 또한, 우리가 #1에서 만들어놓은 Coord[] 배열을 이용해서 접근한다면 쉽게 구할 수 있다.
맵의 1번위치에 있는 구슬을 기준점으로 시작해서 같은 구슬이 나온다면 그 갯수를 Count해주면서 다른 구슬이 나온다면 Count해놓은 갯수가 4이상인지 확인한 후에 구슬을 파괴시켜 주면 된다.
여기서도 똑같이 ! 이 과정에서 구슬을 바로 '0'으로 만들어 주지 않는다. 다만, "파괴될 구슬입니다" 라고 표시만 해줄 뿐이다. 이후에 #3에서 진행했던 구슬을 움직여주는 함수를 그대로 호출해주면 똑같이 구슬일 움직이는 효과를 볼 수 있다.
bool Destroy_Sequence_Marble()
{
memset(Delete, false, sizeof(Delete));
bool Flag = false;
int Cur_Marble = MAP[Coord[1].x][Coord[1].y];
int Sequence_Cnt = 1;
int Start_Num = 1;
int Num;
for (Num = 2; Num < N * N; Num++)
{
int Next_Marble = MAP[Coord[Num].x][Coord[Num].y];
if (Next_Marble == 0) break;
if (Cur_Marble == Next_Marble) Sequence_Cnt++;
else
{
if (Sequence_Cnt >= 4)
{
Flag = true;
for (int i = Start_Num; i < Num; i++) Delete[i] = true;
Marble[Cur_Marble] += Sequence_Cnt;
}
Cur_Marble = Next_Marble;
Sequence_Cnt = 1;
Start_Num = Num;
}
}
if (Sequence_Cnt >= 4)
{
Flag = true;
for (int i = Start_Num; i < Num; i++) Delete[i] = true;
Marble[Cur_Marble] += Sequence_Cnt;
}
return Flag;
}
#5. 맵 정비하기
최종적으로 연속된 구슬의 갯수와 구슬의 번호를 통해서 맵을 다시 만들어 주어야 한다.
이 과정 또한, Coord배열을 이용하고, 1번 위치에 있는 구슬을 기준점으로 시작해서 번호를 증가시켜가면서 탐색을 하면서 진행해 주었다.
void Remake_MAP()
{
int New_MAP[MAX][MAX] = { 0, };
int Cur_Marble = MAP[Coord[1].x][Coord[1].y];
int Cnt = 1;
int Pos_Num = 1;
bool Flag = true;
for (int Num = 2; Num < N * N; Num++)
{
if (Pos_Num >= N * N)
{
Flag = false;
break;
}
int Next_Marble = MAP[Coord[Num].x][Coord[Num].y];
if (Next_Marble == 0) break;
if (Cur_Marble == Next_Marble) Cnt++;
else
{
New_MAP[Coord[Pos_Num].x][Coord[Pos_Num].y] = Cnt;
New_MAP[Coord[Pos_Num + 1].x][Coord[Pos_Num + 1].y] = Cur_Marble;
Cur_Marble = Next_Marble;
Cnt = 1;
Pos_Num += 2;
}
}
if (Flag == true)
{
if (Pos_Num != 1 )
{
New_MAP[Coord[Pos_Num].x][Coord[Pos_Num].y] = Cnt;
New_MAP[Coord[Pos_Num + 1].x][Coord[Pos_Num + 1].y] = Cur_Marble;
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
MAP[i][j] = New_MAP[i][j];
}
}
}
[ 소스코드 ]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
|
#include <iostream>
#include <vector>
#include <cstring>
#define MAX 55
using namespace std;
struct COORD
{
int x;
int y;
};
int N, M, Answer, Marble[4];
int MAP[MAX][MAX];
int N_MAP[MAX][MAX];
bool Delete[MAX * MAX];
COORD Shark;
COORD Coord[MAX * MAX];
vector<pair<int, int>> Cmd;
int dx[] = { 0, -1, 1, 0, 0 };
int dy[] = { 0, 0, 0, -1, 1 };
// 상 하 좌 우
void Input()
{
cin >> N >> M;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> MAP[i][j];
}
}
for (int i = 0; i < M; i++)
{
int a, b; cin >> a >> b;
Cmd.push_back(make_pair(a, b));
}
}
int Change_Dir(int Dir)
{
if (Dir == 1) return 3;
if (Dir == 2) return 4;
if (Dir == 3) return 2;
if (Dir == 4) return 1;
}
void Make_MAP()
{
int x = N / 2;
int y = N / 2;
int Move_Cnt = 1;
int Num = 0;
int Dir = 3;
Shark = { x , y };
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
while (1)
{
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < Move_Cnt; j++)
{
x += dx[Dir];
y += dy[Dir];
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
}
Dir = Change_Dir(Dir);
}
Move_Cnt++;
if (Move_Cnt == N)
{
for (int j = 0; j < Move_Cnt; j++)
{
x += dx[Dir];
y += dy[Dir];
N_MAP[x][y] = Num;
Coord[Num++] = { x , y };
}
break;
}
}
}
void Blizzard_Magic(int Idx)
{
memset(Delete, false, sizeof(Delete));
int Dir = Cmd[Idx].first;
int K = Cmd[Idx].second;
int x = Shark.x;
int y = Shark.y;
for (int i = 0; i < K; i++)
{
x += dx[Dir];
y += dy[Dir];
Delete[N_MAP[x][y]] = true;
}
}
void Move_Marble()
{
bool Flag = false;
int Cnt = 0;
for (int i = 1; i < N * N; i++)
{
if (Delete[i] == true)
{
Flag = true;
Cnt++;
}
else
{
if (MAP[Coord[i].x][Coord[i].y] == 0)
{
for (int j = 1; j <= Cnt; j++) MAP[Coord[i - j].x][Coord[i - j].y] = 0;
Flag = false;
break;
}
else MAP[Coord[i - Cnt].x][Coord[i - Cnt].y] = MAP[Coord[i].x][Coord[i].y];
}
}
if (Flag == true)
{
int i = (N * N) - 1;
for (int j = 0; j < Cnt; j++, i--) MAP[Coord[i].x][Coord[i].y] = 0;
}
}
bool Destroy_Sequence_Marble()
{
memset(Delete, false, sizeof(Delete));
bool Flag = false;
int Cur_Marble = MAP[Coord[1].x][Coord[1].y];
int Sequence_Cnt = 1;
int Start_Num = 1;
int Num;
for (Num = 2; Num < N * N; Num++)
{
int Next_Marble = MAP[Coord[Num].x][Coord[Num].y];
if (Next_Marble == 0) break;
if (Cur_Marble == Next_Marble) Sequence_Cnt++;
else
{
if (Sequence_Cnt >= 4)
{
Flag = true;
for (int i = Start_Num; i < Num; i++) Delete[i] = true;
Marble[Cur_Marble] += Sequence_Cnt;
}
Cur_Marble = Next_Marble;
Sequence_Cnt = 1;
Start_Num = Num;
}
}
if (Sequence_Cnt >= 4)
{
Flag = true;
for (int i = Start_Num; i < Num; i++) Delete[i] = true;
Marble[Cur_Marble] += Sequence_Cnt;
}
return Flag;
}
void Remake_MAP()
{
int New_MAP[MAX][MAX] = { 0, };
int Cur_Marble = MAP[Coord[1].x][Coord[1].y];
int Cnt = 1;
int Pos_Num = 1;
bool Flag = true;
for (int Num = 2; Num < N * N; Num++)
{
if (Pos_Num >= N * N)
{
Flag = false;
break;
}
int Next_Marble = MAP[Coord[Num].x][Coord[Num].y];
if (Next_Marble == 0) break;
if (Cur_Marble == Next_Marble) Cnt++;
else
{
New_MAP[Coord[Pos_Num].x][Coord[Pos_Num].y] = Cnt;
New_MAP[Coord[Pos_Num + 1].x][Coord[Pos_Num + 1].y] = Cur_Marble;
Cur_Marble = Next_Marble;
Cnt = 1;
Pos_Num += 2;
}
}
if (Flag == true)
{
if (Pos_Num != 1 )
{
New_MAP[Coord[Pos_Num].x][Coord[Pos_Num].y] = Cnt;
New_MAP[Coord[Pos_Num + 1].x][Coord[Pos_Num + 1].y] = Cur_Marble;
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
MAP[i][j] = New_MAP[i][j];
}
}
}
void Solution()
{
Make_MAP();
for (int i = 0; i < M; i++)
{
Blizzard_Magic(i);
Move_Marble();
while (1)
{
if (Destroy_Sequence_Marble() == false) break;
Move_Marble();
}
Remake_MAP();
}
Answer = Marble[1] + (2 * Marble[2]) + (3 * Marble[3]);
cout << Answer << endl;
}
void Solve()
{
Input();
Solution();
}
int main(void)
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
//freopen("Input.txt", "r", stdin);
Solve();
return 0;
}
|
cs |